Power Loading

The ratio T/P or the power loading has been previously defined as a rotor efficiency parameter. Helicopters and other rotorcraft are generally designed to hover with the lowest possible power required (and hence lowest fuel bum) for a given gross weight, that is, a high power loading with a large value of T/P is required. Helicopters spend a good proportion of their flight time in hover or low speed forward flight and the use of the hover condition as an initial design point is clear. However, as will be shown in Chapter 6, optimizing the rotor for maximum hovering efficiency can also have some trade-offs in terms of efficient high-speed forward flight performance.

Power loading is the ratio of the thrust produced to the power required to hover, that is,

This quantity should be as close as possible to the ideal value for best hovering efficiency. Because T oc (QR)2 but P oc (QR)2, maximizing the power loading requires a low tip speed (QR). On the basis of simple momentum theory considerations, the ratio P/T is given by

which, as also shown previously in Eq. 2.24, is related to the disk loading. Therefore, to maximize the power loading (that is to minimize the ratio P/T) the disk loading should be low (i. e., the disk area should be large for a given gross weight to give a low induced velocity and the tip speed should be low). Generally, the tip speed is set on the basis of various competing performance requirements for a given rotor size. As shown in Chapter 6, this may include autorotative requirements and rotor noise constraints.

When using the modified momentum theory, the ratio P/T is given by

P T. po

T V IpA + T ‘

Alternatively, we can write

which is a result that depends on the rotor solidity, a. Equation 2.67 can also be written in terms of the figure of merit, that is,

This means that the best rotor efficiency (maximum power loading) is obtained when the disk loading is a minimum and the figure of merit is a maximum.

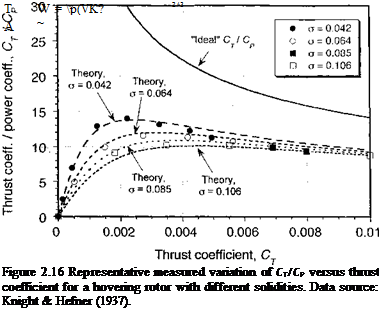
A representative example of the measured CT/CP (which is proportional to power loading at a fixed tip speed) versus thrust is shown in Fig. 2.16 for several values of rotor solidity. By differentiating Eq. 2.67 with respect to CT, it is easy to show that for a rotor with rectangular blades the operating Cp to give the lowest ratio of T/P is

which clearly depends on both the profile and induced effects. Substituting this value into Ea. 2.46, for example, shows that this condition is equivalent to rotor operations at a figure of merit of 2/3к = 0.667к. Using this result, the disk loading for maximum power loading will be at

and for design purposes solving for the rotor radius would determine its optimum value for a given helicopter gross weight, tip speed, and density altitude. However, it is apparent that the conditions for the most efficient operation of the rotor are relatively insensitive to the operating state in that the Ст/Ср (or the T/P) curves in Fig. 2.16 are fairly flat over the normal range of operational thrust coefficients. Therefore, there is some latitude in selecting the rotor radius, which as mentioned previously, may be constrained because of other (nonaerodynamic) factors. See also the discussion in Section 6.4.1.