Power Required in Axial Climbing and Descending Flight
Notice that because the climb and descent velocity changes the induced velocity at the rotor, the induced power will also be affected. In a climb or descent the power ratio is
![]() P_ _ Vc + Vi _ Vc Vi_
P_ _ Vc + Vi _ Vc Vi_
Ph Vh Vh Vh’
The two terms on the right-hand side of the above equation are the work done to change the potential energy of the rotor (helicopter) and the work done on the air by the rotor, respectively. The latter induced loss appears as an increase in dynamic pressure and gain in kinetic energy of the rotor slipstream. Using Eq. 2.81 and substituting and rearranging gives
Climb velocity ratio, V / v
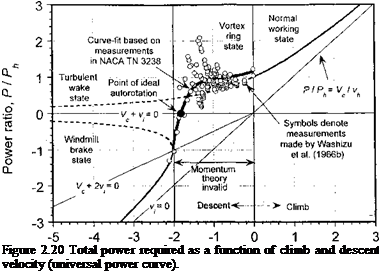 |
c h
the power ratio for a climb as
P V / V 2 V
— = —2- + J ( —— } +1, which is vaiid for — > 0. (2.98)
Ph 2l)/j у 2vh) t>h
In a descent, Eq. 2.91 is applicable, and substituting this into Eq. 2.97 and rearranging gives the power ratio as
Both results are shown in Fig. 2.20, which is usually called the universal power curve – a form first suggested by Lock (1947). This graph shows the total rotor power ratio, P/Ph, plotted versus the climb ratio, Vc/t^. The nonphysical solutions are also shown for reference. Notice that the power required to climb is always greater than the power required to hover. However, as the climb velocity increases the induced power becomes a progressively smaller percentage of the total power required to climb. It is also significant to note that in a descent, at least above a certain rate, the rotor extracts power from the air and uses less power than required to hover (i. e., the rotor now operates like a windmill – see Chapter 13 for more details of this operational state).











