Results

The application of the method to two low pressure turbine rotor bladerows is presented; the two testcases are jointly defined with Duke University, and will be labeled AT and BT.

Complex flitter screening results, obtained through the present method, are compared with the results of a similar method based on CYCLOPS [Kielb and Barter, 2003]; for validation purposes, they are also compared with the aerodamping solution of TACOMA 3D Navier-Stokes time-linearized analysis [Holmes et al., 1997], performed on 3D fhxible modeshapes.

Since overall flitter stability behavior remain rather similar for similar ge­ometries and aerodynamic conditions of LPT blades with pure subsonic fbw [Tchernycheva et al., 2001], it is possible to perform the aeroelastic calcula­tions on a blade and then extend the results to another one, for preliminary design purposes.

In this paper, LARS calculations have been carried out on one section of the BT bladerow, and then used for both AT and BT complex flutter screening.

In figures 2a and 2b, the critical reduced frequency maps obtained on the BT selected section are presented.

Figure 2a. BT bladerow: nearfield criti – Figure 2b. BT bladerow: farfield critical cal reduced frequency map reduced frequency map

For each testcase, two complex mode families have been analyzed: the first will be referred to as ml, the second as m2.

In figure 3 a the aerodynamic damping coefficient is plotted versus the num­ber of nodal diameters for the AT ml mode family. The two INDIAN results are based on Navier-Stokes and Euler aeroelastic calculations: the adopted aerodynamic work normalization is the one described in the appendix. It can be seen that viscous effects do not have much influence on the blade flutter stability.

For comparison purposes, results are also presented in terms of the so-called “ critical damping ratio”, based on the energy normalization described in [Kielb et al., 2003]: in figure 3b INDIAN results are plotted together with CYCLOPS and TACOMA 3D solutions. The two CYCLOPS curves are derived from Euler aeroelastic calculations performed on two different LPT blades; in par-

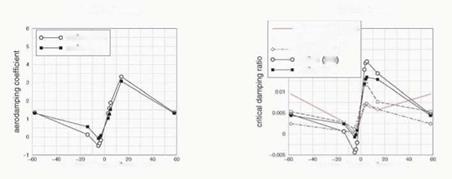In figures 4a and 4b, the same plots are presented for AT m2 modes. Again viscous effects seem to be not very important and INDIAN results agree well with CYCLOPS, especially with the“Cyclops E” curve. For low (positive and negative) nodal diameters the agreement is fairly good with TACOMA 3D results, as well.

In figures 5a and 5b, results for BT m1 mode family are shown. For this blade, only Navier-Stokes based INDIAN results are presented. A generally good agreement is obtained between INDIAN, CYCLOPS and TACOMA;

again the agreement is better for backward traveling waves, and INDIAN tends to overestimate stability for positive nodal diameters.

Figure 5b. BT m1 modes: critical damp­

ing ratio

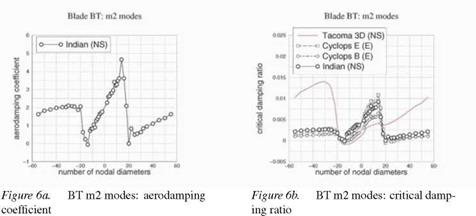Finally, results for BT m2 modes are presented in figures 6a and 6b. Here agreement is satisfactory between INDIAN and CYCLOPS results. Compared with TACOMA solution, the trend is captured in the low nodal diameter re­gion, but the two flitter screening methods consistently over – or underpredict stability in the other regions.

2. Conclusions

A computational method for efficient complex mode flitter screening was described.

This approach exploits a set of aeroelastic time-linearized calculations in order to predict flitter stability of any specified complex mode of the analyzed bladerow and of similar ones. The method was developed for turbomachinery

bladerow design and was applied to two low pressure turbine rotor rows, for test and comparison purposes. From these results it was concluded that the method agrees well with the similar one described in [Kielb and Barter, 2003] for the majority of the examined modes. Both methods were also compared with a 3D time-linearized direct analysis: since they sometimes overestimate aeroelastic stability, flitter screening methods are not always conservative, so they are suitable for preliminary design, but further and more accurate analysis is required during design refinement. Additionally it was found that viscous effects are not very infbent on flitter stability.

Future work is needed to understand if disagreement between flitter screen­ing and 3D calculations is caused by the approximation method adopted to reduce 3D fbxible modeshapes to 2D rigid ones.

Acknowledgments

The authors wish to acknowledge Avio for the financial support and the permission to publish. Special thanks to Prof. E. Camevale (University of Florence) for encouraging this work. The authors wish also to express their gratitude to Prof. R. E. Kielb (Duke University) and J. Barter (GE) for provid­ing testcase data and for some useful suggestions.

Appendix: Normalization for work

Let cw be the aerodynamic work coefficient (that is, the aerodynamic work per unit span divided by mean inlet dynamic pressure and by squared chord).

The aerodamping coefficient is where A represents the vibration non-dimensional ‘amplitude’.

In the traditional definition (see [Boles and Fransson, 1986]) A is the angular amplitude (in radians) for pure torsion or the translational amplitude (divided by the chord) for pure bending. When we deal with arbitrary rigid modes, we must define A in such a way to be consistent with the two mentioned extreme cases, while remaining smooth in the whole range of possible modes. We define

А = Г^кф (A.2)

where кф is the torsional coefficient in the linear combination that defines the mode under examination and / is an appropriate correction factor.

For real modes / must be continuous and positive real (so that it cannot affect the sign of the aerodamping), must tend to one when the torsion axis location Q gets near the airfoil and must tend to zero when Q gets infinitely far from the airfoil in such a way that fDq —► 1 where Dq is the distance of Q from the airfoil, normalized by the chord.

The correction factor proposed by Panovsky and Kielb [Panovsky and Kielb, 2000] is

where xN and yN are two normalized coordinates such that the airfoil LE and ТЕ are placed in (0, 0) and (1,0), respectively. With this factor the desired goal of consistency is not quite reached, since fppDq —> 1/4.

An alternative, fully consistent, correction factor is given by

For complex modes / must be again continuous and positive real and must tend to real mode / when the complex mode degenerates to a real one. For real modes XQ and yq were of course real and derived from the three linear combination real coefficients that describe the vibration mode (hx, hy and hy). In order to extend the correction factor definition to complex modes, we can derive two complex quantities (xq and yq) in a formally identical way, exploiting hx, hy and hy (that are now complex). These two quantities are not coordinates of a point, since they are complex, but their moduli can be used in the previous formulae to compute generalized correction factors.

References

Arnone, A. (1994). Viscous analysis of three-dimensional rotor fbw using a multigrid method. Journal of turbomachinery, 116:435-445.

Boles, A. and Fransson, T. H. (1986). Aeroelasticity in turbomachines Comparison of theoreti­cal and experimental cascade results. Number 13 in Communication du laboratoire de ther – mique appliquee et de turbomachines de Гесоїе polytechnique federale de Fausanne. EPFF.

Fransson, T. H. and Verdon, J. M. (1991). Updated report on “standard configurations for un­steady fbw through vibrating axial-fbw turbomachine-cascades”, <http://www. egi. kth. se/ proj/Projects/Markus%20joecker/STCF/STCFltol0/Documents/SC2110.92update. pdf>.

Giles, M. (1988). Non-refbcting boundary conditions for the euler equations. <http://web. comlab .ox. ac. uk/oucl/work/mike. giles/psfiles/bcs. ps. gz>.

Hall, K. C. and Clark, W. S. (1993). Finearized euler predictions of unsteady aerodynamic loads in cascades. AIAA Journal, 31:540-550.

Holmes, D. G., Mitchell, B. E., and Forence, C. B. (1997). Three dimensional finearized navier – stokes calculations for flitter and forced response. In 8 th International Symposium on Un­steady Aerodynamics and Aeroelasticity in Turbomachines.

Kielb, R. E. and Barter, J. (2003). Flutter design of lpt blades with cyclic symmetry modes – complicating effects. Submitted to ISUAAAT 2003 Conference.

Kielb, R. E., Barter, J., Chernysheva, O., and Fransson, T. H. (2003). Flutter of low pressure turbine blades with cyclic symmetric modes – a preliminary design method. In IGTIASME Turbo Expo.

Marshall, J. G. and Imregun, M. (1996). A review of aeroelasticity methods with emphasis on turbomachinery applications. Journal of fluids and structures, 10:237-267.

Panov sky, J. and Kielb, R. E. (2000). A design method to prevent low pressure turbine blade flitter. Journal of engineering for gas turbines and power, 122:89-98.

Tchernycheva, O. V., Fransson, T. H., Kielb, R. E., and Barter, J. (2001). Comparative analysis of blade mode shape infhence on flitter of two-dimensional turbine blades. In XVISOABE conference.