Rigid Body Mode Shapes

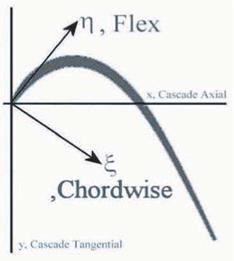
As in Panovsky and Kielb (1998) the three dimensional mode shapes are reduced to a two dimensional rigid body mode shape consisting of two trans­lations and one rotation about the leading edge (See Figure 2).

{

h^ic І Г

hvicand |ais| = < hvis

aic ais

The l subscript defines the nodal diameter, and determines the interblade phase angle, of the mode.

Now consider the term, Wcc.

Wcc — к J (etcPci) • ndA A

ec = h^c<p£ + hqc&q + асфа

ф^, фп are unit vectors in the £ and n directions, respectively фа is a vector in the n direction with an amplitude equal to the distance from the leading edge

Pci — h£cC£i + hqcCqi + ac Cai

The Ci terms are the imaginary parts of the linearized unsteady aerodynamic coefficients. As in Panovsky and Kielb (1998) the work term can then be writ­ten as

Wcc — { h£c hnc ac }	wii	W£n	w^a	( hic
wnS	wnn	wqa	hqc
	_ Wai	wan	waa	[ ac

where Wab = К f ((фаCbi^ • n) dA

By similarity

his

hqs

as J

	= { hc		ac }	wii	w^	w&	( his
Wcs	h hnc	wv^	wnn	wqa	< hns
				_ wJa^	waq	waa	as
wab =	/«	фа Cbr	j • nj dA

The Cr terms are the real parts of the unsteady aerodynamic coefficients. To get the Wsc terms simply interchange the c and s subscripts. In the new method presented herein, these three-by-three work matrices must be generated for a baseline airfoil for a range of interblade phase angles and reduced frequencies. These matrices can then used for a wide range of LPT blade designs.