The Lift-to-Drag Ratio: Aerodynamic Efficiency

Simple concepts from thermodynamics make it clear that creation of lift to balance the weight of the vehicle in flight is not without a penalty. The rule (i. e., First Law of Thermodynamics) that “you cannot get something for nothing” applies here. The drag force is a measure of the cost or penalty function for atmospheric flight. Drag results from complex interactions involving not only friction but also other fun­damental loss effects involved in the lift-generation process. The aerodynamic pen­alty for lift generation is the production of what is called induced drag.

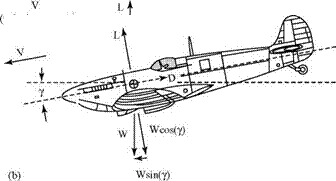
Figure 1.14(a) shows the force balance for a vehicle in level, unaccelerated flight. It is clear that if a particular level flight speed is to be maintained, a force must be introduced to balance the drag force. This is provided by the propulsion system in the form of thrust, T. If the vehicle is to climb or accelerate to a yet higher speed, additional energy must be expended in producing an even higher thrust force, T, to overcome the additional drag. The drag force always acts to retard the motion through the air. Thus, in producing sufficient lift to balance the weight in level flight, energy must be expended to counter the drag. Therefore, a measure of the efficiency of the aerodynamic design is the ratio:

It is obvious that we strive to make this value as large as possible within a set of design constraints and the mission requirements for the vehicle. The range, speed, rate of climb, and many other performance factors depend on achievement of high values for this ratio.

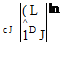Key performance elements depend on how well a designer addresses the many competing requirements. For example, it is shown readily by computing the power required for level flight and determining the rate at which fuel must be consumed to produce this power that the range of a propeller-driven airplane is:

the famous Breguet range equation. In this formula, n is the efficiency of the pro­peller, c is the specific fuel consumption (i. e., rate at which fuel is used to produce the motor power output), and Winitial/Wfinal is the ratio of the initial weight of the airplane to the weight after the fuel has been expended. This result clearly indicates the importance of aerodynamic efficiency in attaining long-range flight.

In the special field of sailplane (i. e., motorless airplane or glider; cf. Figs. 1.14(b) and 1.15) competition, recent research in drag reduction has led to the achievement of lift-to-drag (L/D) ratios approaching 60. The motivations for a high L/D ratio in this application are obvious. In Fig. 1.14(b), notice that in equilibrium, unpow­ered flight, the airplane must fly downward relative to the airmass at the glide angle Y. Therefore, the lift must balance only the cosine component of the weight. The other weight component (proportional to sin y) is required to counteract the drag. A measure of the sailplane performance is the “flatness” of the glide (i. e., smallness of angle y). By equating the balancing-force components, we see that:

L _ Wcosу_ 1 (1.3)

D Wsin у tan y

Therefore, a high L/D ratio means a very flat glide. A sailplane with L/D = 60 can cover a distance of 60 miles while losing only 1 mile of altitude. The glide-slope angle y is less than 1 degree! Thus, the L/D ratio often is referred to as the glide ratio. Much of the work needed to achieve this phenomenal performance was done using mathematical tools and concepts of the type studied in detail in this book, as well as careful wind-tunnel testing of aerodynamic refinements.

Similar attention to drag reduction has led to more economical commercial flight in the transonic flight regime and to higher cruising speeds in the supersonic regime. More complex dependence on lift and drag is involved in those cases.