TRANSFER FUNCTIONS OF GENERAL LINEAR/INVARIANT SYSTEM

The transfer functions of a physical system that exists and is available for testing can be found from experiment, by making suitable measurements of its inputs and outputs. Here we are concerned with obtaining the transfer function by analysis. The experimental method is based in any case on the analytical formalism that we develop in the following. The procedure begins, of course, with the application of the appropriate physical laws that govern the behavior of the system. When the complete set of equations that express these laws has been formulated, it will, for linear/invariant systems, usually appear as a set of coupled differential equations of mixed order. A partic­ularly simple example (the second-order system) was given above, and it demonstrates what may be called the direct method of finding transfer functions. That is, form the Laplace transform of the system equations, just as they naturally occur, and solve for the appropriate ratios. We give a further illustration below for a pair of coupled second-order equations (a fourth-order system), such as might arise in the analysis of a double pendulum, or two massive particles on a stretched string, or two coupled L-R-C circuits, etc. The example equations are

* + «!# + «2* + a3x + a4 у = Л £ + Ky + b2y + b3x + bAy = /2

On forming the Laplace transforms, with

Ф) = 2/(0) = *(0) = 2/(0) = 0

the result is x(s2 + a2s + a3) + ^(cqs2 + a4) = f

z(s2 + b3) + i/(V2 + V + bi) = A

which can readily be solved for the four required transfer functions. We rewrite (3.2,12) as

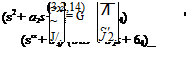(3.2,13)

(3.2,15)

is the matrix of the four transfer functions that relate x and у outputs to Д and /2 inputs. There are however two other state variables, making the required total of four, and consequently there are four more transfer functions to be found. The additional variables are the two rates

x = и y = v

The transforms of (3.2,16) with zero initial values are

sx = и sy = V

whence the four additional transfer functions are [see (3.2,3d)]

G^ = S=*d4=sG*fl <3-2’i7>

Ції vfi

and similarly

Gvf1 = sGvf1> Gv/2 = sGvf2

An alternative procedure for finding the matrix of system transfer functions consists of putting the equations in the standard first-order form. Any rtth- order system of linear equations can be expressed as a set of n first-order equations. Consider (3.2,10) for example. By using (3.2,16) they become

u + axv = a2u – a3x – a^y + Д ^

й + bji = — V — b3x — b4y + /a ’

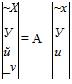which together with (3.2,16) are the required four first-order equations. They are not yet in the standard form, however. For that, one first solves (3.2,18) for и and v, which are linear functions of u, v, x, y, fv and/2. Combining the result with (3.2,16) yields a matrix equation of the form

where A is a 4 X 4 matrix, and C is a 4 x 2 matrix. (The determination of A and C is left as an exercise for the reader.)

Equation (3.2,19) is an example of the canonical form, which for the general linear system is

(3.2,20)

where у is the state и-vector and x the nonautonomous input r-vector. A (an n x n matrix) and C (an n x r matrix) may in general be time depend­ent. Here however, we are confining the discussion to invariant systems, and hence the Laplace transform of (3.2,20) is simply, for y(0) = 0

where I is the identity matrix. It follows that

у = («I – A)_1Cx (3.2,22)

From (3.2,36) we can therefore identify G as

G = (si – A)-*C

It can in principle be evaluated whenever A and C are known.