Unsteady Aerodynamics of Slender Wings

It is also customary to start the unsteady aerodynamic analysis of wings with simple harmonic motion and obtain analytical expressions for the amplitude of the aerodynamic coefficients of the large aspect ratio wings which have elliptical span wise load distribution. In addition, Reissner’s approach for the large aspect ratio rectangular wings numerically provides us with the aerodynamic characteristics. As a more general approach, the doublet lattice method handles wide range of aspect ratio wings with large sweeps and with span wise deflection in compressible subsonic flows. In later chapters, the necessary derivations and representative examples of these methods will be provided.

1.1 Compressible Steady Aerodynamics

It is a well known fact that at high speeds comparable with the speed of sound the effect of compressibility starts to play an important role on the aerodynamic characteristics of airfoil. At subsonic speeds, there exists a similarity between the compressible and incompressible external flows based on the Mach number M = U/аж, аж = free stream speed of sound. This similarity enables us to express the compressible pressure coefficient in terms of the incompressible pressure coefficient as follows

Po

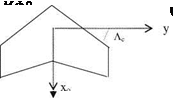
Fig. 1.4 Prandtl-Glauert transformation, before M = 0, and after M = 0

Here,

o

is the surface pressure coefficient for the incompressible flow about a wing which is kept with a fixed thickness and span but stretched along the flow direction, x, with the following rule

x

xo = — ; yo = y, Zo = z

1 – M2

as shown in Fig. 1.4. The Prandtl-Glauert transformation for the wings is sum­marized by Eq. 1.14 and Eq. 1.13 is used to obtain the corresponding surface pressure coefficient. By this transformation, once we know the incompressible pressure coefficient at a point x, y, z, Eq. 1.13 gives the pressure coefficient for the known free stream Mach number at the stretched coordinates xo, yo, zo. As seen from Fig. 1.4, it is not practical to build a new plan form for each Mach number. Therefore, we need to find more practical approach in utilizing Prandtl-Glauert transformation.

For this purpose, assuming that the free stream density does not change for the both flows, we integrate Eq. 1.13 in chord direction to obtain the same sectional lift coefficient for the incompressible and compressible flow. While doing so, if we keep the chord length same, i. e., divide xo with (1-M2)1/2, then the compressible sectional lift coefficient cl and moment coefficient cm become expressible in terms of the incompressible clo and cmo as follows

The result obtained with Eq. 1.15a, b is applicable only for the wings with large aspect ratios and as the aspect ratio gets smaller the formulae given by 1.15 a, b fails to give correct results. For two dimensional flows Eq. 1.15a, b gives good results before approaching critical Mach numbers. The critical Mach number is the free stream Mach number at which local flow on the airflow first reaches the speed of sound. Equations 1.15a, b are known as the Prandtl-Glauert compressibility correction and they give the compressible aerodynamic coefficients in terms of the Mach number of the flow and the incompressible aerodynamic coefficients. The drag coefficient, on the other hand, remains the same until the critical Mach number is reached.

The total lift coefficient for the finite thin wings with the sectional lift slope ao, and aspect ratio AR reads as

Formula 1.16 is applicable until the critical Mach number is reached at the surface of the wing.

In case of finite wings, there is a way to increase the critical Mach number by giving sweep at the leading edge. If the leading edge sweep angle is Л, then the sectional lift coefficient at angle of attack which is measured with respect to the free stream direction, reads as

ao cos Л

— a

1 — M2 cos2 Л

The effect of Mach number and the sweep angle combined reduces the sectional lift coefficient as compared to the wings having no sweep. Now, if we consider the aspect ratio of the finite wing, the Diederich formula becomes applicable for the total lift coefficient for considerably wide range of aspect ratios,

1 — M2

cos Ле = — cos Л.

1 — M2 cos2 Л

For the case of supersonic external flows, we encounter a new type of aerodynamic phenomenon wherein the Mach cones whose axes are parallel to the free stream send the disturbance only in downstream. The lifting pressure coefficient for a thin airfoil, in terms of the mean camber line z = za(x), reads as

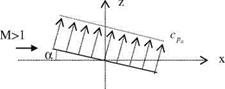
Fig. 1.5 Supersonic lifting pressure distributions along the flat plate

Figure 1.5 gives the lifting pressure coefficient distribution for a flat plate at angle of attack a.

In order to obtain the sectional lift for the flat plate airfoil we need to integrate Eq. 1.19 along the chord

4a

Pm2 – 1

The sectional moment coefficient with respect to a point whose coordinate is a on the chord reads

Using Eqs. 1.20 and 1.21, the center of pressure is found at the half chord point as opposed to the quarter chord point for the case of subsonic flows. The effect of compressibility on the sectional lift coefficient is shown in Fig. 1.6 with the necessary modification near M = 1 area.

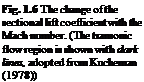An important characteristic of the supersonic flow is its wavy character. The reason for this is the hyperbolic character of the model equations at the supersonic speeds. The emergence of the disturbances with wavy character from the wing surface requires certain energy. This energy appears as wave drag around the airfoil. The sectional wave drag coefficient can be evaluated in terms of the equations for the mean camber line and the thickness distribution along the chord as follows.

1

—4

л/M2 – 1

-1

According to Eq. 1.22 the sectional drag coefficient is always positive and this is in agreement with the physics of the problem.