Work for General Complex Mode Shapes

Work per cycle can be calculated by integrating the dot product of the local velocity vector with the local force vector over one cycle of vibration and the entire airfoil surface.

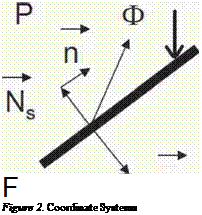Airfoil Surface

4 = velocity N = normal vector P = surface pressure

For harmonic motion the displacement, normal vector and surface pressure can be written as (the bar over the variables indicates the complex conjugate)

Ф = І (фе~іиі + феіші)

N = Ns + і (пе~ш + Heiojt)

P = Ps + (pe~iujt + peiut)

The work per cycle then becomes

For real mode shapes the work per cycle reduces to the familiar expression

Thus the steady pressure term does not contribute to the work when the mode shape is real. As will be shown, this is not the case when the mode shape is complex.

2. Work for Cyclic Symmetry Mode Shapes

For cyclic symmetry eigensolutions the mode shapes are complex. For a forward traveling wave

ф=(ас – ias) n = nc — ins

Where ac and as are commonly referred to as the cosine and sine modes. The work per cycle becomes

Wcyc — 7Г J Ns * ificPimag H – &sPreal) Ps ific * ^s &s * ^c)

A L

Thus, the work has a component associated with the unsteady pressure and a component associated with the steady pressure.

WCyc — WUp + Wps