A comparison of steady and unsteady flow

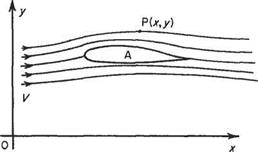
Figure 2. la shows a section of a stationary wing with air flowing past. The velocity of the air a long way from the wing is constant at V, as shown. The flow parameters are measured at some point fixed relative to the wing, e. g. at P(x, y). The flow perturb­ations produced at P by the body will be the same at all times, i. e. the flow is steady relative to a set of axes fixed in the body.

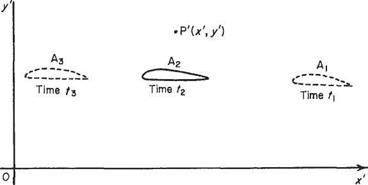
Figure 2.1b represents the same wing moving at the same speed V through air which, a long way from the body, is at rest. The flow parameters are measured at a point P’C*’, /) fixed relative to the stationary air. The wing thus moves past P7. At times t, when the wing is at A, P’ is a fairly large distance ahead of the wing, and the perturbations at P’ are small. Later, at time t2, the wing is at Аг, directly beneath P7, and the perturbations are much larger. Later still, at time Гз, Ґ is far behind the wing, which is now at Аз, and the perturbations are again small. Thus, the perturbation at P’ has started from a small value, increased to a maximum, and finally decreased back to a small value. The perturbation at the fixed point P’ is, therefore, not constant with respect to time, and so the flow, referred to axes fixed in the fluid, is not steady. Thus, changing the axes of reference from a set fixed relative to the air flow, to a different set fixed relative to the body, changes the flow from unsteady to steady. This produces the

mathematical simplification mentioned earlier by eliminating time from the equations. Since the flow relative to the air flow can, by a change of axes, be made steady, it is sometimes known as ‘quasi-steady’.