ADDITIONAL PHYSICAL CONSIDERATIONS

The above mathematical formulation, even after selecting a desirable com­bination of sources and doublets and after fulfilling the boundary conditions on the surface SB, is not unique. As we have seen in the previous chapters, for lifting flow conditions the magnitude of circulation depends on the wake shape and on the location of the wake shedding line and, therefore, an appropriate wake model needs to be established. Following the practice of the previous chapters, the wake model will be based on some additional physical conditions (e. g., the Kutta condition) as follows.

FIGURE 13.2

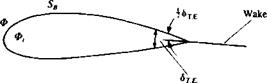Possible assumption for wake shape near the trailing edge.

The validity of this assumption depends on the component of the kinematic velocity, normal to the trailing edge, which must be much smaller than the characteristic velocity (e. g., Qr) for Eq. (13.20) to be valid (see additional discussion of this condition in Section 13.11).

Also the Kelvin condition can be used to calculate the change in the wake circulation

f = 0 (.3,6)

Wake shape. Following the requirement of Section 9.3, that the wake is force-free, the Kutta-Joukowski theorem (Section 3.11) states that:

QXYw = 0 (13.21)

where Q is the total velocity. When the wake is modeled by a vortex distribution of strength Yw, Eq. (13.21) can be interpreted as a requirement that the velocity should be parallel to the circulation vector

Q II Yw (13.21a)

Also, in most cases the trailing edge has a finite angle and an additional assumption has to be made about the angle at which the wake leaves the trailing edge. In these cases it is usually sufficient to assume that the wake leaves the trailing edge at a median angle dT B J2, as shown in Fig. 13.2.