Aeroelastic Model

Let assume that the blades are non-twisted with a constant cross-sectional area along the blade length. The centre of shear and gravity of the blade cross­sections coincide. Let us consider the motion of nth blade as plane motion of the solid body with two degrees of freedom. The transverse displacements of the nth blade in x, y directions (hXn, hyn) are described as:

hxn (t) = hxо sin[w„t + (n – 1)6]

hyn (t) = hyo sin[cunt +(n – 1)5],

and angular displacements of the nth blade an(t):

an(t) = a0 sin[cjnt + (n – 1)5]. (1)

Here hXQ, hyo, ao are the amplitudes of oscillations the same for all blades; un is oscillation angular frequency of the nth blade; 5 is the constant interblade phase angle; n is the blade number.

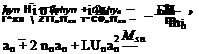The equations of motion are reduced to set of three ordinary linear differen­tial equations of first order for only torsion (an) and bending(/ixn, hyn). For a constant force F0 acting during a period At one obtains the linear differential equations of second order with the constant coefficients for n-th blade:

where nn is a damping parameters.

The 3D unsteady transonic fbw of an ideal gas is described by the Euler equations, represented as conservation laws in an arbitrary Cartesian coordi­nate system, rotating with the constant angular velocity uo (see Gnesin and Rzadkowski 2000):

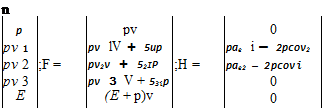Here p and p are the pressure and density; tq, vs are the velocity

nents; aei and ae2 are the transfer acceleration projections; e = P U + r2a;2 is the total energy of volume unit; є is an internal energy of mass unit; r is the distance from the rotation axis.

The above system of equations is completed by the perfect gas state equation

Р = є(х~ 1),

where x denotes the ratio of the fhid specific heats.

The spatial solution domain is discretized using linear hexahedral elements.

The 3D Euler equations are integrated on moving H-H (or H-O) – type grid with use of explicit monotonous second – order accuracy Godunov – Kolgan difference scheme.