Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
An Analysis of Blade Vibration Instability
The tip section of Quiet Fan B in NASA Quiet Engine Program [6], shown in Fig.4, was adopted as the cascade model for the present analysis. Figure 5 shows the computed steady Mach contours in the case when inlet Mach number is 1.25, and the static pressure ratio (po/pi, i;inlet, o;outlet) is 1.7. A passage shock wave generated at the trailing edge of each blade can be clearly seen in flow channels. Concerning vibration instability of this cascade model, the oscillation of the passage shock wave is known to be the most influential factor. An oblique shock is generated at the leading edge of each blade, and impinges to the suction surface of the adjacent blade.
|
|
|
|
 |
|
|
|
|
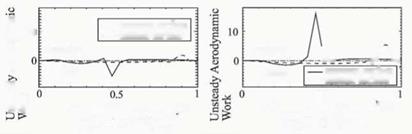
Figure 7. Unsteady Aerodynamic Work Distribution on the Blade Surface
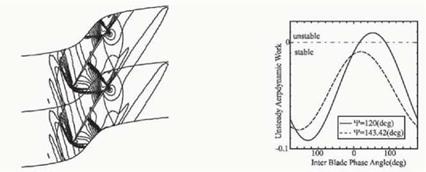
The blade vibration instability was investigated in the above ft>w field. The blade was forced to oscillate with the reduced frequency of 0.084. The direction of blade motion, Ф, was 143.42 degrees (case 1) and 120 degrees (case 2). Since a realistic blade is designed in a three-dimensional manner, the stagger angle is different in the spanwise direction. The difference of stagger angle results in the change in the direction of blade oscillation at each spanwise section of the blade. It is reported that the oscillation direction plays an important role for the blade vibration instability in the transonic ft>w condition [7].
The inflience coefficient method [8] was used for analysis of blade vibration instability. Figure 6 shows the result of instability analysis by this method when the reduced frequency is 0.084. The horizontal axis is the inter blade phase angle, while the vertical axis corresponds to the unsteady aerodynamic work on a blade. Blade vibration is unstable when the aerodynamic work is positive. As shown in Fig.6, blade vibration was always stable in the case 1. In the results of the case 2, on the other hand, the blade oscillation was unstable around 90 degrees of inter blade phase angle.
Figure 7 shows the chordwise unsteady aerodynamic work distribution on the blade surface when all blades were forced to oscillate with 90 degrees of inter blade phase angle. Figure 7(a) shows the results of the case 1, while Fig. 7(b) shows those of the case 2. At the part where the unsteady aerodynamic work is positive, the unsteady aerodynamic force acts as exciting force. In the results of Fig. 7(a), a negative peak can be seen at around 50% chord position on the pressure surface. The peak is caused by the oscillation of passage shock. In the result of the case 2, Fig. 7(b), the peak is observed to be positive, which means that the unsteady aerodynamic work induced by passage shock movement becomes exciting one. The characteristics of unsteady aerodynamic force thus differ depending on the blade oscillation direction. The unsteady aerodynamic work due to the shock oscillation is revealed to be dominant for blade vibration instability in the result, because the value of the peak is larger than that at another position on the blade surface. On the suction surface, on the
other hand, a positive peak is observed at around 90% chord position both in the case 1 and case 2. The peak is caused by the oscillation of the oblique shock impinges there from the leading edge of the neighboring blade.
