Bernoulli equation

If the flow is irrotational, then the velocity must be the gradient of a velocity potential ф(r, t).

V = Vф (1.102)

If f is the gravitational force per unit mass as is usually case, then we also have

f = —g Vz (1.103)

where g is gravity’s acceleration and z is the vertical height. With these assumptions, and also assum­

ing that the flow is effectively inviscid so r can be neglected, the alternative form of the compressible or incompressible momentum equation (1.91) or (1.86) simplifies to

V4 + Jv(V2) = – gVz – ^ (1.104)

dt 2 p

which can be integrated if we make suitable assumptions about the density p.

Incompressible Bernoulli equation

Assuming p = constant and integrating (1.104) gives the general Incompressible Bernoulli equation

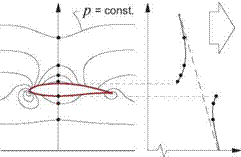
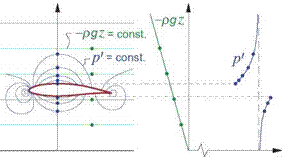
Figure 1.15: Overall pressure p decomposed into hydrostatic and dynamic components — pgz + p’.

where C is some integration constant. It is convenient to decompose the pressure p into a hydrostatic pressure field —pgz and a remaining part p’ associated with only the fluid motion, as shown in Figure 1.15.

p = —pgz + p’ (1.106)

This effectively eliminates the gravity term from the Bernoulli equation (1.105).

% + + t = c

dt 2 p

From now on we will denote p’ simply as “p ” with the understanding that it really represents the deviation from the known hydrostatic pressure —pgz. The latter provides a buoyancy force equal to the displaced fluid’s weight, which directly adds to the hydrodynamic force from p’ and surface viscous stresses.

Fbuoyancy = © pgz n dS = pgz dV = pg Vbody z (1.108)

body body

This buoyancy force is usually ignored, notable exceptions being lighter-than-air and underwater vehicles.

This pressure decomposition is not usable for the free-surface flows about surface water vehicles. Here the overall true pressure —pgz + p’ is imposed to be constant on the free surface as a boundary condition, which then results in the generation of surface gravity waves with heights z. These waves influence the velocity field, which in turn influences p’ and hence the wave shapes. Therefore, the hydrostatic and dynamic parts of the pressure field are two-way coupled and cannot be treated separately.

Pc + 2pV* = po-

For low-speed steady aerodynamic flows, the constant C in (1.107) is most conveniently defined from the known freestream total pressure, giving the most familiar form of the Bernoulli equation.

In this case, the pressure coefficient definition (1.54) also reduces to a relatively simple form.

V 2

cr = i-w

It must be stressed that the Bernoulli forms (1.109) and (1.110) apply only where the total pressure is equal to the freestream value.

Compressible Bernoulli equation

An alternative assumption for the density is to use the isentropic relation (1.69)

in which case (1.104) integrates to the compressible version of the general Bernoulli equation.

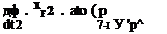,2 / m (Y-1)/Y

+ gz = C

7-1 * r2( V2 2 дф 2 M c2 v2 dt

Dropping the gravity term as before, and using the freestream to evaluate the integration constant gives the isentropic unsteady pressure formula, with the steady form obtainable by dropping the дф/dt term.