Blade Element Analysis in Hover and Axial Flight

The blade element approach for the analysis of helicopter rotors has been well established in the prior literature – see Payne (1959), Bramwell (1976), Johnson (1980), and Prouty (1986). The resultant local flow velocity at any blade element at a radial distance у from the rotational axis has an out-of-plane component Up — Vc + normal to the rotor as a result of climb and induced inflow and an in-plane component Up = Ely parallel to the rotor because of blade rotation, relative to the disk plane. The resultant velocity at the blade element is, therefore,

U = yju2 + U2P. (3.1)

The relative inflow angle (or induced angle of attack) at the blade element will be (Vr Up „ …

ф = tan * і — і ^ — tor small angles. (J. z)

Up / ‘ Up

Thus, if the pitch angle at the blade element is в, then the aerodynamic or effective AoA is

Up

a = в — ф = в—– -. (3.3)

Up

The resultant incremental lift dL and drag dD per unit span on this blade element are

1 9 1 9

dL = – pU2cCi dy and dD = ~pU2cCd dy, (3.4)

where Ci and Cd are the lift and drag coefficients, respectively. The lift dL and drag dD act perpendicular and parallel to the resultant flow velocity, respectively. Notice that the quantity c is the local blade chord. Using Fig. 3.1 these forces can be resolved perpendicular and parallel to the rotor disk plane giving

dFz = dLcosф — dDsinф and dFx = dL sin0 + dD cos0. (3.5)

Therefore, the contributions to the thrust, torque, and power of the rotor are

dT = NbdFz, dQ = NbdFxy and dP = NbdFxQy, (3.6)

where Nb is the number of blades comprising the rotor. Notice that in the hover or axial flight condition, the aerodynamic environment is (ideally) axisymmetric and the airloads
are independent of the blade azimuth angle. Substituting the results for d Fx and d Fz from Eq. 3.5 gives

dT = Nb(dL cos0 — dD sin0),	(3.7)
dQ – Nb(dL sinф + dD cosф)у,	(3.8)
dP — Nb(dL sinф + dDcosф)Qy.	(3.9)

For helicopter rotors the following simplifying assumptions can be made:

1. The out-of-plane velocity Up is much smaller than the in-plane velocity Uj, so that U = yjUj + Up ~ Ut – This is a valid approximation except near the blade root, but the aerodynamic forces are small here anyway.

2. The induced angle ф is small, so that ф = Up/Ut – Also, sin ф — ф and cos ф = 1.

3. The drag is at least one order of magnitude less than the lift, so that the contribution dDsїnф (or dDф) is negligible.

Applying these simplifications to the preceding equations results in

dT = NbdL,	(3.10)
dQ = NbUf)dL + dD)y,	(З. И)
dP = NbQ(4>dL +dD)y.	(3.12)

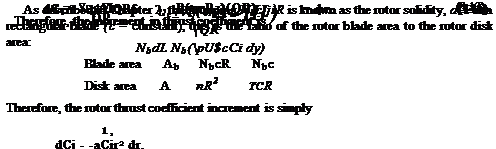Proceeding further, it is convenient to introduce nondimensional quantities by dividing lengths by R and velocities by QR. Hence, r = у/R, and Uj QR = Qy/QR — y/R = r. Also, dCT = dT/pA(QR)2, dCQ = dQ/pA(QR)2R, and dCP = dP/pA(QR)3. The inflow ratio can be written as

This is one of the most fundamental equations for rotating-wing analysis by means of the BET. By a similar approach, it can be shown that the rotor-torque coefficient increment is

dQ Nb(si>dL + dD)y 1

~ pA{SlR)2R ~ p(TtR2)(QR)2R ~ 2

= (ФСі + Cd)r3 dr, which will be noted to represent the sum of an induced part and a profile part.

3.2.1 Integrated Rotor Thrust and Power

To find the total Cj and Cq, the incremental thrust and power quantities derived above must be integrated along the blade from the root to the tip. For a rectangular blade, the thrust coefficient is

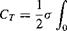(3.17)

where the limits of integration are r — 0 at the root to г = 1 at the tip. For the corresponding torque or power coefficient

using the general result that ф = Xfr from Ea. 3.13.

To evaluate Cj and Cp it is necessary to predict the spanwise variation in the inflow, X, as well as the sectional aerodynamic force coefficients, С/ and Cd. If 2-D aerodynamics are assumed, then С/ = C/(a, Re, M) and Cd — Cd(a, Re, M), where Re and M are the local Reynolds number and Mach number, respectively (see Chapter 7). Also, a = a(Vc, 0, Vi) and u, — u,(r). Because these effects cannot, in general, be expressed as simple analytic results, it is necessary to numerically solve the integrals for Cp and Cp. However, with certain assumptions and approximations, it is possible to find closed-form analytical solutions. These solutions are very useful because they serve to illustrate the fundamental form of the results in terms of the operational and geometric parameters of the rotor. They also provide exact check cases for the numerical solutions to the blade element theory.