Blade Element Momentum Theory (BEMT)

The blade element momentum theory (BEMT) for hovering rotors is a hybrid method that was first proposed for helicopter use by Gustafson & Gessow (1946) and Gessow (1948) and combines the basic principles from both the blade element and momentum theory approaches. The principles involve the invocation of the equivalence between the circulation and momentum theories of lift. With certain assumptions, the BEMT allows the inflow distribution along the blade to be estimated.

Consider first the application of the conservation laws to an annulus of the rotor disk, as shown in Fig. 3.4- This is the essence of Froude’s original differential theory for pro-

прііргс in qyi q1 mritinn TVne annulne і c at о Hicfon^A лі fmm іЬа rAfotinnal ovic onrl

J 111 U/V1U1 11IV/1,1 vy 11. 1 lUO UUUU1UO Ш Ul U U1JIUUV/V у 11 V/J 11 IUV 1 J LUUWl IU1 ci/yio, шш

has a width dy. The area of this annulus is, therefore, dA = 2ny dy. The incremental thrust, dT, on this annulus may be calculated on the basis of simple momentum the­ory and with the 2-D assumption that successive rotor annuli have no mutual effects on each other. As might be expected, this approach has good validity except near the blade tips. The removal of this 2-D restriction requires a considerably more advanced treatment of the problem using a vortex wake theory. However, a good approximation to the tip-loss effect on the inflow distribution can be made using Prandtl’s “circulation – loss” function, which will be discussed in Section 3.3.10. Tokaty (1971) gives a good historical overview of the origins of the blade element and blade element momentum theories.

On the basis of simple one-dimensional momentum theory developed in Chapter 2, we may compute the incremental thrust on the rotor annulus as the product of the mass flow rate through the annulus and twice the induced velocity at that section. In this case the mass flow rate over the annulus of the disk is

dm = pdA(Vc + Vi) = 2np(Vc + Vi)y dy, so that the incremental thrust on the annulus is

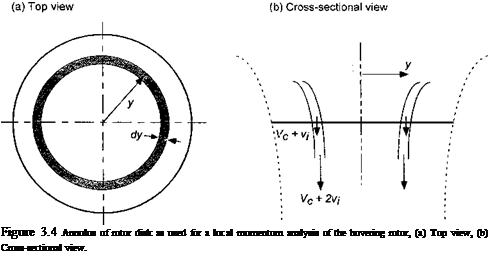dT = 2p (Vc + vi) vtdA = Anp (Vc + v{) v{y dy.

This has also been known as the Froude-Finsterwalder equation. It is more convenient to work in nondimensional quantities so that

_ dT_________ _ 2p{Vc + Vi)vjdA

T ~ pin R2)(QR)2 ~ pjrRHQR)2

– 2p(Vc + ьіЇьі(27ТУ dy) _ + Vi) / Vi / y Y y

pnR2(QR)2 ~ QR Qr)r) r)

or simply

dCT = 4АА/Г dr, (3.44)

Therefore, the incremental thrust coefficient on the annulus can be written as

dCj = 4AA, r dr = 4A (A — Ac)r dr (3.45)

because А і — A — Ac. The induced power consumed by the annulus is

dCpi = A dCj = 4A2A, r dr = 4A2 (A — Ac)r dr. (3.46)

This assumes no swirl in the wake, which is justified in Section 3.3.6. Consider first the hovering state where Ac = 0. The incremental thrust and power contributions of the annulus are given by

dCp = 4A2r dr and dCpt = 4A3r dr,