Crocco relation

The d() differentials in the Gibbs relation (1.61) can be taken along a dx interval and then divided by dx to convert them to partial derivatives.

ds dh 1 dp

dx dx p dx

Repeating this along dy and dz intervals, and adding the three results as vector components, gives the gradient form of the Gibbs relation.

TVs = Vh – ^ p

1 p

= у ho – – V(V-V)————- (1.99)

2 p

Combining this with the alternative form of the momentum equation (1.91) gives

dV 1 _

TVs = Vh0 + ^————– Vxw – f – – V • r (1.100)

dt p

which for steady inviscid flow without body forces simplifies to the Crocco relation.

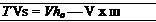(steady, inviscid) (1.101)

For the steady adiabatic case this explicitly confirms the equivalence between isentropy and irrotationality deduced in the previous section. It is also useful in many applications in which one of the three terms in (1.101) is known explicitly, which then provides an explicit relation between the two remaining terms.