Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
DESCRIBING FUNCTION
 |
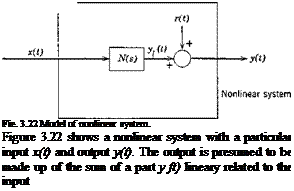In the simplest terms, a describing function of a system is a transfer function that linearly connects an input/output pair approximately—i. e. it provides a linear approximation to the actual system that is best in a certain sense.
Vi(s) = N{s)x(s)
and a remnant r(t) that makes up the difference. Clearly, if r(t) is “small” enough compared to y(t), then у ft) provides a useful evaluation of the system performance. When an appropriate measure of r(t) is minimized, N(s) becomes the corresponding describing function. For transient inputs, a suitable measure would be J r2 dt; for steady-state inputs, periodic or stochastic (the usual case treated), r2 is the quantity minimized. It is seen that a different describing function is obtained for every input to a given system—i. e. the describing function, unlike the transfer function of a linear system, is a function of the input.
