DEVELOPMENT OF AERODYNAMIC PITCHING MOMENTS
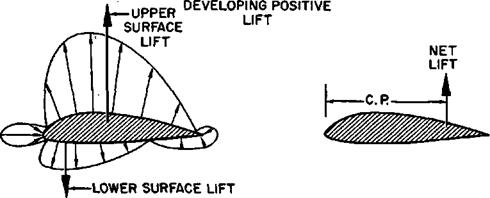
The distribution of pressure over a surface is the source of the aerodynamic moments as well as the aerodynamic forces. A typical example of this fact is the pressure distribution acting on the cambered airfoil of figure 1.21. The upper surface has pressures distributed which produce the upper surface lift; the lower surface has pressures distributed which produce the lower surface lift. Of course, the net lift produced by the airfoil is difference between the lifts on the upper and lower surfaces. The point along the chord where the distributed lift is effectively concentrated is termed the “center of pressure, c. p." The center of pressure is essentially the “center of gravity” of the distributed lift pressure and the location of the c. p. is a function of camber and section lift coefficient.
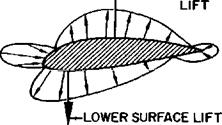
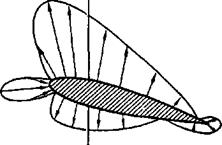
Another aerodynamic reference point is the “aerodynamic center, a. c.” The aerodynamic center is defined as the point along the chord where all changes in lift effectively take place. To visualize the existence of such a point, notice the change in pressure distribution with angle of attack for the symmetrical airfoil of figure 1.21. When at zero lift, the upper and lower surface lifts are equal and located at the same point. With an increase in angle of attack, the upper surface lift increases while the lower surface lift decreases. The – change of lift has taken place with no change in the center of pressure—a characteristic of symmetrical airfoils.
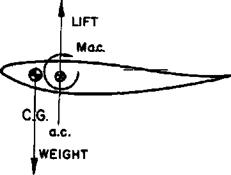
Next, consider the cambered airfoil of figure 1.21 at zero lift. To produce zero lift, the upper and lower surface lifts must be equal. One difference noted from the symmetrical airfoil is that the upper and lower surface lifts are not opposite one another. While no net lift exists on the airfoil, the couple produced by the upper and lower surface lifts creates a nose down moment. As the angle of attack is increased, the upper surface lift increases while the lower surface lift decreases. While a change in lift has taken place, no change in moment takes place about the point where the lift change occurs. Since the moment about the aerodynamic center is the product of a force (lift at the c. pJ) and a lever arm (distance from c. p. to an increase in lift moves the center of pressure toward the aerodynamic center.
It should be noted that the symmetrical airfoil at zero lift has no pitching moment about the aerodynamic center because the upper and
|
 SYMMETRICAL AIRFOIL
SYMMETRICAL AIRFOIL
AT ZERO LIFT
|
|
|
|
|
|

SYMMETRICAL AIRFOIL
AT POSITIVE LIFT
CAMBERED AIRFOIL AT POSITIVE LIFT
|
|
|
|
|
|
|
![]()

lower surface lifts act along the same vertical line. An increase in . lift on the symmetrical airfoil produces no change in this situation and the center of pressure remains fixed at the aerodynamic center.
The location of the aerodynamic center of an airfoil is not affected by camber, thickness, and angle of attack. In fact, two-dimensional incompressible airfoil theory will predict the aerodynamic center at the 25 percent chord point for any airfoil regardless of camber, thickness, and angle of attack. Actual airfoils, which are subject to real fluid flow, may not have the lift due to angle of attack concentrated at the exact 25 percent chord point. However, the actual location of the aerodynamic center for various sections is rarely forward of 23 percent or aft of 27 percent chord point.
The moment about the aerodynamic center has its source in the relative pressure distribution and requires application of the coefficient form of expression for proper evaluation. The moment about the aerodynamic center is expressed by the following equation :
АІВ. С.=CMa e qSc
where
e = moment about the aerodynamic center, a. c., ft.-lbs.
CM = coefficient of moment about the a. c.
a. c,
q=dynamic pressure, psf T=wing area, sq ft. c=chord, ft.
The moment coefficient used in this equation is the dimensionless ratio of the moment pressure to dynamic pressure moment and is a function
r h/ia. c.
мал— q$c
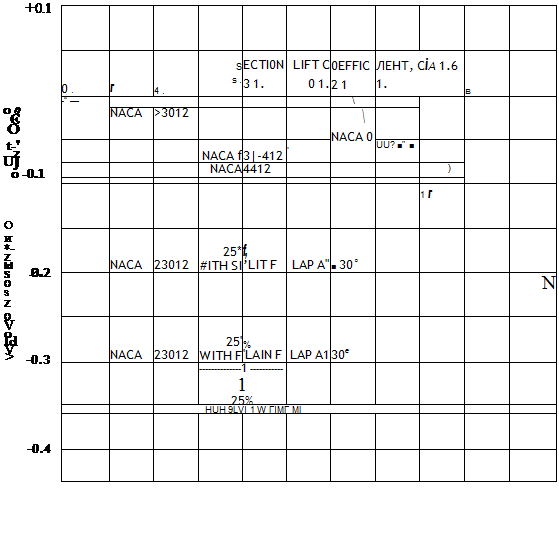
of the shape of the airfoil mean camber line. Figure 1.22 shows the moment coefficient,
cmae versus lift coefficient for several representative sections. The sign convention applied to moment coefficients is that the nose-up moment is positive.
The NACA 0009 airfoil is a symmetrical section of 9 percent maximum thickness. Since the mean line of this airfoil has no camber, the coefficient of moment about the aerodynamic center is zero, i. e., the c. p. is at the a. c. The departure from zero стл, е, occurs only as the airfoil approaches maximum lift and the stall produces a moment change in the negative (nose-down) direction. The NACA 4412 and 63i~412 sections have noticeable positive camber which cause relatively large moments about the aerodynamic center. Notice that for each section shown in figure 1.22, the fmeie. is constant for all lift coefficients less than ci.
max
The NACA 23012 airfoil is a very efficient conventional section which has been used on many airplanes. One of the features of the section is a relatively high with only a small c„a e The pitching moment coefficients | for this section are shown on figure 1.22 along with the effect of various type flaps added to the basic section. Large amounts of camber applied well aft on the chord cause large negative moment coefficients. This fact is illustrated by the large negative moment coefficients produced by the 30° deflection of a 25 percent chord flap.
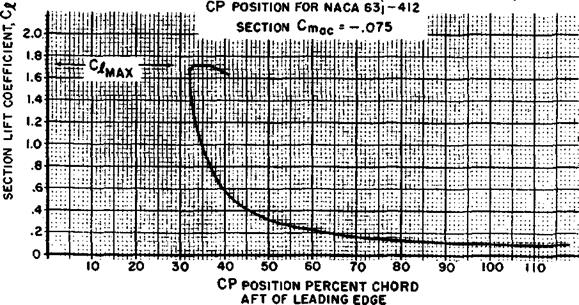
The cma e is a quantity determined by the shape of the mean-camber line. Symmetrical airfoils have zero c„ac and the c. p. remains at the a. c. in unstalled flight. The airfoil with positive camber will have a negative cmae which means the c. p. is behind the a. c. Since ther,^ is constant in unstalled flight a certain relationship between lift coefficient and center of pressure can be evolved. An example of this relationship is shown in figure 1.22 for the NACA 63i~412 airfoil by a plot of c. p. versus Cj. Note that at low lift coefficients the center of pressure is well aft—even past the trailing edge—and an increase in ct moves the c. p. forward toward the ax. The c. p. approaches the
 |
|
|
|
|
|
ax. as a limit but as stall occurs, the drop in suction near the leading edge, cause the c. p. to move aft.
Of course, if the airfoil has negative camber, or a strongly reflexed trailing edge, the moment about the aerodynamic center will be positive. In this case, the location of the aerodynamic center will be unchanged and will remain at the quarter-chord position.
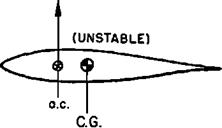
The aerodynamic center is the point on the chord where the coefficients of moment arc constant—the point where aJl changes in lift take place. The aerodynamic center is an extremely important aerodynamic reference point and the most direct application is to the longitudinal stability of an airplane. To simplify the problem assume that the airplane is a tailless or flying wing type. In order for this type airplane to have longitudinal stability, the center of gravity must be ahead of the
aerodynamic center. This very necessary fea~ ture can be visualized from the illustrations of figure 1.23.
If the two symmetrical airfoils are subject to an upgust, an increase in lift will take place at the ax. If the c. g. is ahead of the ax., the change in lift creates a nose down moment about the c. g. which tends to return the airfoil to the equilibrium angle of attack. This stable, "weathercocking” tendency to return to equilibrium is a very necessary feature in any airplane. If the c. g. is aft of the ax., the change in lift due to the upgust takes place at the a. c. and creates a nose up moment about the c. g. This nose up moment tends to displace the airplane farther from the equilibrium and is unstable—the airplane is similar to a ball balanced on a peak. Hence, to have a stable airplane, the c. g. must be located ahead of the airplane a. c.
An additional requirement of stability is that the airplane must stabilize and be trimmed for flight at positive lift. When the c. g. is located ahead of a. c., the weight acting at the c. g. is supported by the lift developed by the section. Negative camber is required to produce the positive moment about the aerodynamic center which brings about equilibrium or balance at positive lift.
Supersonic flow produces important changes in the aerodynamic characteristics of sections. The aerodynamic center of airfoils in subsonic flow is located at the 25 percent chord point. As the airfoil is subject to supersonic flow, the aerodynamic center changes to the 50 percent chord point. Thus, the airplane in transonic flight can experience large changes in longitudinal stability because of the large changes in the position of the aerodynamic center.