ELEMENTARY AERODYNAMICS

A real fluid is viscous and compressible. But, if the speed of flow is much less than the speed of propagation of sound, the variation of density caused by the motion of a body in the flow is so small that the fluid may be regarded as incompressible. Furthermore, for fluids like water and air, the effects of viscosity are felt only in a thin layer (the boundary layer) next to the solid wall of the body. Outside the boundary layer the fluid may be regarded as nonviscous. A nonviscous and incompressible fluid is called a perfect fluid. In many problems of aeroelasticity, it is sufficient

to consider the fluid as a perfect fluid. However, there are cases in which the viscosity, however small, has profound effects, for it controls the boundary layer which may become detached from part of the solid body, and thus affects the macroscopic picture of the flow.

The force, exerted by the fluid on a body situated in a flow, does not depend on the absolute velocity of either the fluid or the body, but only on the relative velocity between them. The aerodynamic force consists of two components: the pressure force normal to the surface of the body, and the skin friction, or shearing force, tangential to the surface of the body. The latter is often negligible in aeroelastic problems.

In order to determine the parameters, on which depends the force that acts on a body situated in a flow, a dimensional analysis can be made. Obviously the force depends on the geometry of the body and its attitude relative to the flow; these, for geometrically similar bodies, can be characterized by a typical length / and a typical angle «. The force will also depend on the density of the fluid p, the viscosity of the fluid p, the speed of flow U, the compressibility of the fluid, and the nonstationary characteristics of the flow. The last item can be expressed in a clear-cut way if the conditions of flow happen to be periodic. In a periodic oscillation, the frequency со characterizes the nonstationary feature. The compressibility of the fluid may be expressed in various ways. A simple index of the compressibility is the speed of propagation of sound in the fluid, because sound is propagated as longitudinal elastic waves.

Let the speed of sound propagation be denoted by c. Then, in an oscillating flow of a compressible fluid, the force experienced by a solid body will depend on the following variables:

l, a, p, U, p, со, c

A dimensional analysis shows that, for geometrically similar bodies, the force F acting on the body can be expressed as

(1)

where f is a function of the variables contained inside the parentheses. It is easy to verify that the parameters Ulpjp, toljU, and Ujc are all dimensionless numbers.

The following notations will be used throughout this book:

M = — = Mach number c

q = pVi— dynamic pressure

The parameters R, k, and M are named in honor of O. Reynolds, V. Strouhal, and E. Mach, respectively. The factor v = /лір is called the kinematic viscosity.

The speed of sound propagation in a gas is given by the equation

where p is the static pressure, p is the density, and у is the ratio of the specific heat at constant pressure to the specific heat at constant volume. For dry air, у = 1.4. Using the equation of state, we obtain

c=VyRJ

where Rg denotes the gas constant. For air, the above equation becomes

c = A9.WT

where T is in degrees Rankine. At the standard conditions at sea level, c = 1130 ft per sec.

For air under standard conditions of temperature and pressure: p — 0.002378 slug per ft3 at 15° C and 760 mm Hg v — 0.0001566 ft2 per sec at 15° C and 760 mm Hg

For water under the same conditions, v = 1.228 x 10-5 ft2 per sec. More complete data of the physical properties of air and water can be found in Refs. 1.51, and 2.25. For approximate mental calculation, the following formulas may be useful:

Dynamic pressure at sea level:

Reynolds number in air at sea level:

R = 10,000 (U in mph) (/ in ft)

In aeroelasticity we are concerned primarily with two components of force and one component of moment that act on a body. These are:

Lift — L — force perpendicular to the direction of motion

Drag = D — force in the direction of motion, positive when the force acts in the downstream direction

Pitching moment = M — moment about an axis perpendicular to both the direction of motion and the lift vector, positive when it tends to raise the leading edge of the body

When airplane wings or complete airplanes are considered, the mean chord c of the wing is usually taken as the characteristic length, and the wing area S the characteristic area. The three primary airplane coefficients are:

CL = lift/(<p§) = lift coefficient

CD = drag/(ipS) = drag coefficient (3)

Су = pitching moment/qSc — pitching-moment coefficient

CL, CD, and CM are functions of the Reynolds number, Mach number, Strouhal number, and the body’s shape and attitude with respect to the flow. For an airfoil, the attitude is described by the angle between the direction of motion U and a reference axis called the chord line. This angle, denoted by a, is called the angle of attack.

In a steady flow of an incompressible fluid, the Strouhal number and the Mach number both vanish, and CL, CD, Су depend on R and a alone. In the remainder of this section, unless mentioned otherwise, we shall consider only the steady, incompressible case.

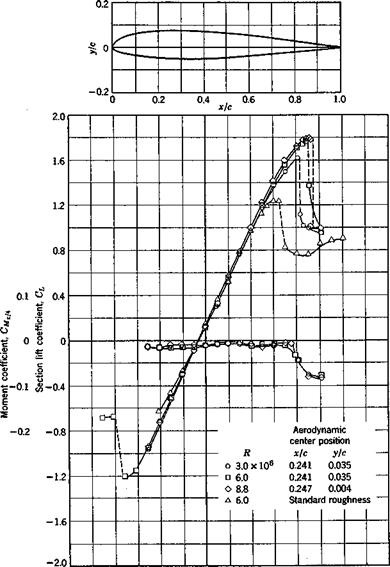
The variation of the coefficients CL, CD, and CM with a is illustrated for a typical airfoil in Fig. 1.11. When a is small, CL increases linearly with a. The proportional constant is called the lift-curve slope and is denoted by a. When a becomes larger, the lift curve begins to level off and finally drops downward. The wing is then said to have stalled. The lift-curve slope a is nearly independent of the Reynolds number.

Let v be the fluid velocity at any point along a closed path of integration, dl an element of length along the path, and в the angle between v and dl. Then the circulation Г around the given path is defined as the line integral of v cos в:

Г = § v cos в dl (4)

The fundamental importance of the concept of circulation may be roughly stated by the fact that, in a perfect fluid, with constant total pressure and in steady motion, the circulation is identical around every simple closed path enclosing a given set of solid bodies. Thus the circulation around a body has a unique and well-defined meaning, independent of the choice

-24 -16 -8 0 8 16 24 32

Section angle of attack, a, degrees

Fig. 1.11. Lift and moment characteristics for the NACA 23012 airfoil. The moment is taken about a point located at V4-chord length behind the leading edge. The aerodynamic center location is computed from CL and CMrti data. The Reynolds number is seen to affect mainly the maximum lift coefficient. (From Abbott, von Doenhoff, and Stivers, NACA Rept. 824. Courtesy of the NACA.)

that may be made of the particular path used for calculating the value of the circulation.

A type of singularity in a fluid called a vertex line is a curve around which the circulation is a constant. A vortex line cannot end itself in a fluid; it must either form a closed’curve or extend to infinity, or else end on a free surface or a solid boundary. A free vortex, one on which no external force acts, is transported with the fluid; i. e., it moves with the flow. On the other hand, a bound vortex, one that moves relative to the flow, requires the action of external forces to maintain such relative motion. As mentioned before, in a steady flow, the circulation about a solid body is a constant. For a steady, two-dimensional flow of a perfect fluid about an infinitely long cylindrical body of any cross sectional shape whatever, the following can be proved theoretically:

(a) The drag is zero.

(b) In the absence of circulation around the body, the lift is zero.

(c) If there is a circulation of magnitude Г around the body, and if the body moves with a rectilinear velocity U relative to the fluid at infinity, then a lift exists, whose magnitude per unit length perpendicular to the flow is given by Joukowsky’s theorem:

L = PUY (5)

where p is the density of the fluid. The direction of the lift is normal both to the velocity U and the axis of the cylinder.

It is clear that, as far as the lift is concerned, the solid body may be replaced by a bound vortex line. For an unstalled airfoil, the circulation Г around it varies linearly with the angle of attack a. If a is measured from the zero-lift attitude which corresponds to Г = 0, then Г ~ L ~ a, and the lift coefficient can be expressed as

CL == a0 a (6)

The angle of attack thus measured is called the absolute angle of attack. The word “absolute” is sometimes omitted. It is understood throughout this book that, when we speak of an angle of attack, we mean the absolute angle of attack. If a is measured in radians (1 radian = 57.3°), hydro – dynamic theory gives the lift-curve slope

a0 = 2я – (theory, incompressible fluid) (7)

for thin airfoils in a two-dimensional flow. Experimental values of the lift-curve slope may be expressed in the form

a0 = 2ttij (8)

The correction factor rj is called the airfoil efficiency factor, which is less
than 1 («a 0.9) for conventional airfoil sections, but is greater than 1 for NACA low-drag sections.

According to the theory of thin airfoils in a two-dimensional incom­pressible fluid, the center of pressure of the additional lift due to change of a is located at V4-chord aft of the leading edge. This point is called the aerodynamic center. If the moment coefficient is computed about the aerodynamic center, it does not vary with CL. The symbol Сш or CMcti is used to denote the moment coefficient referred to an axis located at the V4-chord point. The aerodynamic center remains close to the 1/4-chord point in a compressible fluid as long as the flow is subsonic, but it moves close to the mid-chord point if the flow is entirely supersonic.

The subscript 0 of the lift-curve slope a0 signifies that a0 is the value pertaining to an airfoil of infinitely long span. For wings of finite span

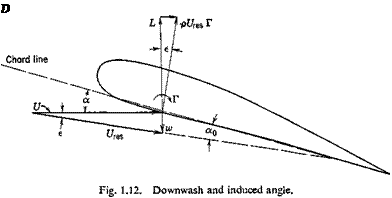
the lift-curve slope is smaller. In Prandtl’s finite-wing theory, a wing is replaced by a vortex line. Since a vortex line cannot end at the wing tip, it must continue laterally out of the wing and become a free vortex (trailing vortex) in the fluid. The vertical velocity w induced by the trailing vortices is called the induced velocity. Because of the induced velocity, the direction of flow at the airfoil is changed by an amount e, which is given by the relation

tan e = w/U (9)

From Fig. 1.12 it is seen that the effective angle of attack a,, is smaller than the geometric angle of attack a. Assuming that w is infinitesimal compared with U, we may write

The resultant force р[/гевГ acts in a direction normal to the resultant

velocity vector Ures. It can be resolved into a lift component L perpen­dicular to the velocity of flow U and a drag component (induced drag) D in the direction of U. Prandtl assumes that the circulation Г is pro­portional to the effective angle of attack a„. By using Eq. 6 relating CL (and hence Г) with a0, and expressing the downwash w in terms of the spanwise-lift distribution, a relation between the lift coefficient CL and the geometrical angle of attack a can be derived.

The final result takes a particularly simple form if the wing planform is an elongated ellipse and is untwisted (having a constant angle of attack across the span). In this case the lift distribution across the span is elliptical, with a principal axis at the mid-span. The special properties associated with the elliptic lift distribution are that (1) the downwash is constant across the span, and (2) for a given total lift, span, and speed of flow the induced drag has its lowest possible value. For an elliptic lift distribution,

From the relations

CL = a0 a,, = aa.

and Eq. 10, one obtains the lift-curve slope of a wing of finite span:

a — ——– °° —■■ (elliptic lift distribution) (15)

1 + (a0/vJR)

For nonelliptic lift distribution, the downwash is no longer constant across the span. Equation 15 is modified as follows:

a = ———- —, ———- (nonelliptic) (16)

1 + (aJvJRX 1 + r)

where t is a small correction factor depending on the deviation of the lift distribution from the ideal elliptical form. Figure 1.13 shows the value of t as calculated by Glauert for straight-tapered, untwisted wings of aspect ratio Ж = 2тг. JRe is the effective aspect ratio. If the lift is symmetrically distributed over the span, JRe is given by Eq. 12. If the
lift is antisymmetrically distributed over the span (as induced by an anti- symmetrical deflection of the ailerons), with zero lift at the mid-span, then Re should be taken as half of the actual JR. Hence,

JRe = JR (for symmetrical lift distribution)

JRe = JR/2 (for antisymmetrical lift distribution) (17)

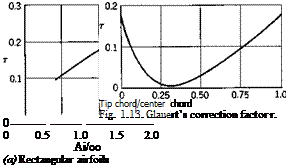Such a correction of aspect ratio is necessary because Eq. 16 is derived for an untwisted wing. The correction (Eq. 17) is plausible, because each of the two halves of the antisymmetrical lift distribution appears similar to an elliptic distribution with a span equal to half of the actual wing span.

(b) Tapered airfoils with Л1 = oq (= 2ir)

Some important characteristic quantities of airfoils, such as the profile drag coefficient C/x>> the maximum lift coefficient CL max, the moment coefficient at zero lift Сш, the angle of zero lift are only of minor importance in aeroelasticity. They do not appear in most of the problems. On the other hand, the question of spanwise lift distribution corresponding to a twisted airfoil is of great importance in aeroelasticity. For mathe­matical simplicity, we shall often use the so-called strip theory as a first approximation. In this, one assumes that the local lift coefficient Сг(у) is proportional to the local geometric angle of attack a(y):

CM = aa.{y) (18)

The effect of finite span is then to be corrected by using a value of a corrected for aspect ratio.[3]

Finally, the principle of superposition must be mentioned. In aero­dynamics, the fundamental equations are essentially nonlinear, and so the superposition principle is valid only in special cases. However, in the airfoil theory, it is often assumed that the disturbance in the flow due to the presence of an airfoil is infinitesimal; i. e., the velocity induced by the solid body is infinitesimal in comparison with the speed of the undisturbed flow, and the hydrodynamic equations can be linearized. In this case the superposition is permissible.