Categories

Special Recent Posts

Our heavyweight helicopter equal in the world does not have

Our heavyweight helicopter equal in the world does not have

In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
In Italy broke experimental tiltrotor

In Italy broke experimental tiltrotor

The experimental military man конвертоплан, developed by "August Vestland's" company, brok[...]
The old plane — nonsense, pilots think - there was an attack

The old plane — nonsense, pilots think - there was an attack

In spite of the fact that the main version of crash of the Russian plane of the Kogalymavia company [...]
The Israeli Apache will subject to peeling

The Israeli Apache will subject to peeling

The Israeli shock Boeing AH-64 Apache helicopters will undergo "peeling" procedure. As rep[...]
The aviation industry began to move

The aviation industry began to move

On Monday against Dubai Airshow air show - the 2015th Deputy Prime Minister Dmitry Rogozin blew up t[...]

Example of Design Problem

Posted by admin in Theoretical and Applied Aerodynamics on February 5, 2016

Design the simplest airfoil (thin cambered plate) such that the center of pressure stays at the quarter-chord at all incidences (small a’s) and the design lift (Cl)des > 0 is obtained at the angle of adaptation aadapt. By simplest airfoil, we mean one that has the smallest number of non zero Fourier coefficients. This has a practical interest for a “flying wing” configuration, where the long fuselage providing a moment from the tail is not available to balance the pitching moment at different incidences.

Example of Design Problem

The condition reads

 

Xc. p. A0 + A1 — “2r 1

C 4 (A0 + 4

 

(3.87)

 

Upon multiplying by the denominator (not zero, since C; = 0), one finds

 

A2 = A1

 

(3.88)

 
Example of Design Problem

x x 2

d (x) = a — A0 + A 2 — 10 + 8 2

 

(3.90)

 

Integrating from 0 to x gives

 
Example of Design Problem

(3.91)

 

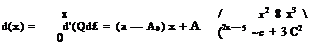The condition that d (c) = 0 determines A0 = a — A. Substitution of this result in the expression of the lift coefficient results in Ci = 2n (a + – A). Finally, the equation of the camberline can be factorized as

d(x) = Ax (7 — 80 (l — 0 (3.92)

From the previous result, the ideal angle of attack is aadapt = A and the associated lift (Ci)adapt = nA = (Ci)des. This determines the unknown coefficient A:

 

A (Cl)des

n

 

(3.93)

 

A sketch of the thin cambered plate at incidence of adaptation is shown in Fig. 3.23.

 

Fig. 3.23 Thin cambered plate at design conditions

 

z

 

L’

 

U

 

x

 

c_

4

 

a

 

c

 

0

 

Example of Design Problem

Example of Design Problem



Related Posts: