First Approximation to the Power Required to Hover

The actual power is the induced power divided by the Figure of Merit:

I D. L.

, _ h’.p_ T J 2p

‘P’“ F. M. 550 (F. M.)

At sea level, this becomes:

Ту/РЇ.

■p’act 38 (F. M.)

The power loading in pounds per horsepower can be obtained by rearranging the equation:

T 38 (F. M.)

h-p-aa y/D. L.

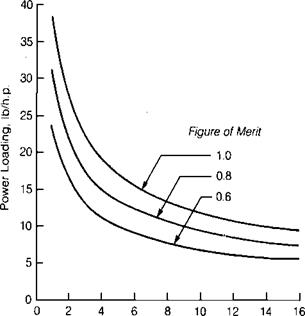
A plot of this equation is presented in Figure 1.4 for Figure of Merit values of 1.0, 0.8, and 0.6—corresponding to the ideal rotor, to a very good practical rotor, and to an average rotor respectively. (Note: A low Figure of Merit in hover does not necessarily represent a poorly designed rotor. More commonly, it represents a rotor that has been designed for high-speed flight and is not being operated at its optimum hovering conditions.) It may be seen from Figure 1.4 that high power loadings go with low disc loadings and high Figures of Merit. The use of this chart allows a first approximation to be made of the power required to hover. The example helicopter has a disc loading of 7.1 lb/ft2. If a Figure of Merit of 0.8 is assumed for its rotor, then the power loading is 11.4 lb/h. p. and, since the helicopter weighs 20,000 lb, the power required by the rotor is 1,760 hp. If the rotor radius had been 40 feet instead of 30, the disc loading would have been 4.0 lb/ft2, and the power required would have been only 1,320; but the tail boom would have had to be 10 feet longer to achieve clearance between main and tail rotors, and the nose would have had to be longer to balance the tail boom. As a

consequence, the reduction in power required would have been obtained at the expense of added structural weight and a larger overall size with, perhaps, little increase in payload capability. Making decisions on this type of trade-off represents much of the engineering effort during the early stages of the development of a new helicopter design.