FRICTION EFFECTS

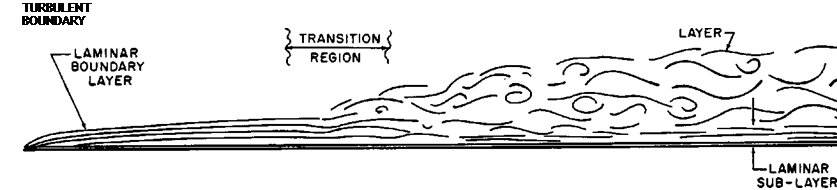
Because the air has viscosity, air will en­counter resistance to flow over a surface. The viscous nature of airflow reduces the local velocities on a surface and accounts for the drag of skin friction. The retardation of air particles due to viscosity is greatest immedi­ately adjacent to the surface. At the very sur­face of an object, the air particles are slowed to a relative velocity of near zero. Above this area other particles experience successively smaller retardation until finally, at some dis­tance above surface, the local velocity reaches the full value of the airstream above the sur­face. This layer of air over the surface which shows local retardation of airflow from vis­cosity is termed the “boundary layer.” The characteristics of this boundary layer are illus­trated in figure 1.24 with the flow of air over a smooth flat plate.

The beginning flow on a smooth surface gives evidence of a very thin boundary layer with the flow occurring in smooth laminations. The boundary layer flow near the leading edge is similar to layers or laminations of air slid­ing smoothly over one another and the obvi­ous term for this type of flow is the “laminar"

boundary layer. This smooth laminar flow exists without the air particles moving from a given elevation.

As the flow continues back from the leading edge, friction forces in the boundary layer continue to dissipate energy of the airstream and the laminar boundary layer increases in thickness with distance from the leading edge. After some distance back from the leading edge, the laminar boundary layer begins an oscillatory disturbance which is unstable. A waviness occurs in the laminar boundary layer which ultimately grows larger and more severe and destroys the smooth laminar flow. Thus, a transition takes place in which the laminar boundary layer decays into a “turbu­lent" boundary layer. The same sort of – transition can be noticed in the smoke from a cigarette in still air. At first, the smoke ribbon is smooth and laminar, then develops a definite waviness, and decays into a random turbulent smoke pattern.

As soon as the transition to. the turbulent boundary layer takes place, the boundary layer thickens and grows at a more rapid rate. (The small scale, turbulent flow within the boundary layer should not be confused with the large scale turbulence associated with airflow separation.) The flow in the turbu­lent boundary layer allows the air particles to travel from one layer to another producing an energy exchange. However, some small lami­nar flow continues to exist in the very lower levels of the turbulent boundary layer and is referred to as the “laminar sub-layer." The turbulence which exists in the turbulent bound­ary layer allows determination of the point of transition by several means. Since the turbu­lent boundary layer transfers heat more easily than the laminar layer, frost, water, and oil films will be removed more rapidly from the area aft of the transition point. Also, a small probe may be attached to a stethoscope and positioned at various points along a surface. When the probe is in the laminar area, a low “hiss” will be heard; when the probe is in

DEVELOPMENT OF BOUNDARY LAYER
ON A SMOOTH FLAT PLATE

COMPARISON OF VELOCITY PROFILES
FOR LAMINAR AND TURBULENT BOUNDARY LAYERS

TURBULENT

PROFILE

— LOW THICKNESS

— LOW VELOCITIES NEXT TO SURFACE

— GRADUAL VELOCITY CHANGE

— LOW SKIN FRICTION

— GREATER THICKNESS

— HIGHER VELOCITIES NEXT TO SURFACE

— SHARP VELOCITY CHANGE

— HIGHER SKIN FRICTION

the turbulent area, a sharp "crackling” will be audible.

In order to compare the characteristics of the laminar and turbulent boundary layers, the velocity profiles (the variation of boundary layer velocity with height above the surface) should be compared under conditions which could produce either laminar or turbulent flow. The typical laminar and turbulent pro­files are shown in figure 1.24. The velocity profile of the turbulent boundary layer shows a much sharper initial change of velocity but a greater height (or boundary layer thickness) required to reach the free stream velocity. As a result of these differences, a comparison will show:

(1) The turbulent boundary layer has a fuller velocity profile and has higher local velocities immediately adjacent to the sur­face. The turbulent boundary layer has higher kinetic energy in the airflow next to the surface.

(2) At the surface, the laminar boundary layer has the less rapid change of velocity with distance above the plate. Since the shearing stress is proportional to the velocity gradient, the lower velocity gradient of the laminar boundary layer is evidence of a lower friction drag on the surface. If the conditions of flow were such that either a turbulent or a laminar boundary layer could exist, the laminar skin friction would be about one-third that for turbulent flow.

The low friction drag of the laminar bound­ary layer makes it quite desirable. However, the transition tends to take place in a natural fashion and limit the extensive development of the laminar boundary layer.

REYNOLDS NUMBER. Whether a lam­inar or turbulent boundary layer exists depends on the combined effects of velocity, viscosity, distance from the leading edge, density, etc. The effect of the most important factors is combined in a dimensionless parameter called "Reynolds Number, RN." The Reynolds Number is a dimensionless ratio which por­trays the relative magnitude of dynamic and viscous forces in the flow.

where

RN= Reynolds Number, dimensionless

V— velocity, ft. per sec.

at= distance from leading edge, ft.

v = kinematic viscosity, sq. ft. per sec.

While the actual magnitude of the Reynolds Number has no physical significance, the quantity is used as an index to predict and correlate various phenomena of viscous fluid flow. When the RN is low, viscous or fric­tion forces predominate; when the RN is high, dynamic or inertia forces predominate. The effect of the variables in the equation for Reynolds Number should be understood. The RN varies directly with velocity and distance back from the leading edge and inversely with kinematic viscosity. High RN’s are obtained with large chord surfaces, high velocities, and low altitude; low RN’s result from small chord surfaces, low velocities, and high altitudes— high altitudes producing high values for kine­matic viscosity.

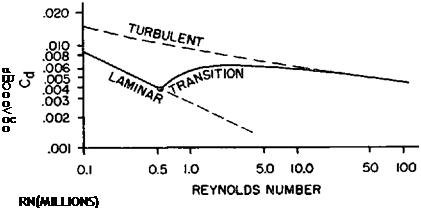
The most direct use of Reynolds Number is the indexing or correlating the skin friction drag of a surface. Figure 1.25 illustrates the variation of the friction drag of a smooth, flat plate with a Reynolds Number which is based on the length or chord of the plate. The graph shows separate lines of drag coeffi­cient if the flow should be entirely laminar or entirely turbulent. The two curves for lam­inar and turbulent friction drag illustrate the relative magnitude of friction drag coefficient if either type of boundary layer could exist. The drag coefficients for either laminar or tur­bulent flow decrease with increasing RN since the velocity gradient decreases as the boundary layer thickens.

FRICTION DRAG OF A SMOOTH
FLAT PLATE

CONVENTIONAL AND LAMINAR
FLOW SECTIONS

TRANSITION

If the surface of the plate is smooth and the original airstream has no turbulence, the plate at low Reynolds Numbers will exist with pure laminar flow. When the RN is increased to approximately 530,000, transition occurs on the plate and the flow is partly turbulent. Once transition takes place, the drag coefficient of the plate increases from the laminar curve to the turbulent curve. As the RN approaches very high values (20 to 50 million) the drag curve of the plate approaches and nearly equals the values for the turbulent curve. At such high RN the boundary layer is predominantly turbulent with very little laminar flow—the transition point is very close to the leading edge. While the smooth, flat plate is not ex­actly representative of the typical airfoil, basic fluid friction phenomena are illustrated. At RN less than a half million the boundary layer will be entirely laminar unless there is extreme surface roughness or turbulence induced in the airstream. Reynolds Numbers between one and five million produce boundary layer flow which is partly laminar and partly turbulent. At RN above ten million the boundary layer characteristics are predominantly turbulent.

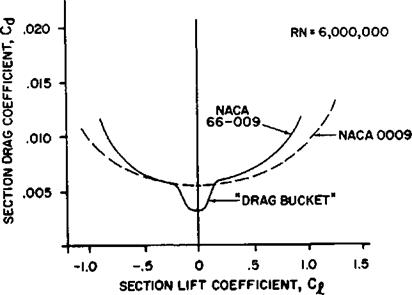
In order to obtain low drag sections, the transition from laminar to turbulent must be delayed so that a greater portion of the sur­face will be influenced by the laminar bound­ary layer. The conventional, low speed air­foil shapes are characterized by minimum pressure points very close to the leading edge. Since high local velocities enhance early transition, very little surface is covered by the laminar boundary layer. A comparison of two 9 percent thick symmetrical airfoils is presented in figure 1.25- One section is the “conventional” NACA 0009 section which has a minimum pressure point at approxi­mately 10 percent chord at zero lift. The other section is the NACA 66-009 which has a minimum pressure point at approximately 60 percent chord at zero lift. The lower local velocities at the leading edge and the favor­able pressure gradient of the NACA 664)09 delay the transition to some point farther aft on the chord. The subsequent reduction in friction drag at the low angles of attack ac­counts for the “drag bucket" shown on the graphs of ct and ct for these sections. Of course, the advantages of the laminar flow airfoil are apparent only for the smooth airfoil since surface roughness or waviness may pre­clude extensive development of a laminar boundary layer.

AIRFLOW SEPARATION. The character of the boundary layer on an aerodynamic surface is greatly influenced by the pressure gradient. In order to study this effect, the pressure distribution of a cylinder in a perfect fluid is repeated in figure 1.26. The airflows depict a local velocity of zero at the forward stagnation point and a maximum local velocity at the extreme surface. The airflow moves from the hieh oositive oressure to the minimum

л. J.

pressure point—a favorable pressure gradient (high to low). As the air moves from the extreme surface aft, the local velocity decreases to zero at the aft stagnation point. The static pressure increases from the minimum (or max­imum suction) to the high positive pressure at the aft stagnation point—an adverse pres­sure gradient (low to high).

The action of the pressure gradient is such that the favorable pressure gradient assists the boundary layer while the adverse pressure gradient impedes the flow of the boundary layer. The effect of an adverse pressure gradi­ent is illustrated by the segment X-Y of figure

1.26. A corollary of the skin friction drag is the continual reduction of boundary layer energy as flow continues aft on a surface. ‘ The velocity profiles of the boundary layer are shown on segment Х-У of figure 1.26. In the area of adverse pressure gradient the bound­ary layer flow is impeded and tends to show a reduction in velocity next to the surface. If the boundary layer does not have sufficient kinetic energy in the presence of the adverse pressure gradient, the lower levels of the boundary layer may stagnate prematurely.

SHOCK WAVE INDUCED
FLOW SEPARATION

NAVWEPS 00-80T-80 BASIC AERODYNAMICS

Premature stagnation of the boundary layer means that all subsequent airflow will overrun this point and the boundary layer will separate from the surface. Surface flow which is aft of the separation point will indicate a local flow direction forward toward the separation point— a flow reversal. If separation occurs the posi­tive pressures are not recovered and form drag results. The points of separation on any aero­dynamic surface may be noted by the reverse flow area. Tufts of cloth or string tacked to the surface will lie streamlined in an area of unseparated flow but will lie forward in an area behind the separation point.

The basic feature of airflow separation is stagnation of the lower levels of the boundary layer. Airflow separation results when the lower levels of the boundary layer do not have sufficient kinetic energy in the presence of an adverse pressure gradient. The most outstanding cases of air­flow separation are shown in figure 1.26. An airfoil at some high angle of attack creates a pressure gradient on the upper surface too severe to allow the boundary layer to adhere to the surface. When the airflow does not adhere to the surface near the leading edge the high suction pressures are lost and stall occurs. When the shock wave forms on the upper surface of a wing at high subsonic speeds, the increase of static pressure through the shock wave creates a very strong obstacle for the boundary layer. If the shock wave is sufficiently strong, separation will follow and “compressibility buffet’’ will result from the turbulent wake or separated flow.

In order to prevent separation of a boundary layer in the presence of an adverse pressure gradient, the boundary layer must have the highest possible kinetic energy. If a choice is available, the turbulent boundary layer would be preferable to the laminar boundary layer because the turbulent velocity profile shows higher local velocities next to the surface. The most effective high lift devices (slots, slotted flaps, BUT) utilize various techniques to increase the kinetic energy of the upper sur­face boundary layer to withstand the more severe pressure gradients common to the higher lift coefficients. Extreme surface roughness on full scale aircraft (due to surface damage, heavy frost, etc.) causes higher skin friction and greater energy loss in the boundary layer. The lower energy boundary layer may cause a noticeable change in CL ^ and stall speed. In the same sense, vortex generators applied to the surfaces of a high speed airplane may allay compressibility buffet to some degree. The function of the vortex generators is to create a strong vortex which introduces high velocity, high energy air next to the surface to reduce or delay the shock induced separation. These examples serve as a reminder that separation is the result of premature stagnation of the boundary layer—insufficient kinetic energy in the presence of an adverse pressure gradient.

SCALE EFFECT. Since the boundary layer friction and kinetic energy are dependent on the characteristics of the boundary layer, Reynolds Number is important in correlating aerodynamic characteristics. The variation of the aerodynamic characteristics with Reynolds Number is termed “scale effect” and is ex­tremely important in correlating wind tunnel test data of scale models with the actual flight characteristics of the full size aircraft. The two most important section characteristics affected by scale effects are drag and maximum lift—the effect on pitching moments usually being negligible. From the known variation of boundary layer characteristics with Rey­nolds Number, certain general effects may be anticipated. With increasing Reynolds Num­ber, it may be expected that the section maxi­mum lift coefficient will increase (from the higher energy turbulent boundary layer) and that the section drag coefficient will decrease (similar to that of the smooth plate). These effects are illustrated by the graphs of figure

1.27.

The characteristics depicted in figure 1.27 are for the NACA 4412 airfoil (4 percent

a0 , DEGREES C£

camber at 40 percent chord, 12 percent thick­ness at 30 percent chord)—a fairly typical “conventional" airfoil section. The lift curve show a steady increase in гг_м with increasing RN. However, note that a smaller change in Ci occurs between Reynolds Numbers of 6.0 and 9.0 million than occurs between 0.1 and

3.0 million. In other words, greater changes in ci occur in the range of Reynolds Num­bers where the laminar (low energy) boundary layer predominates. The drag curves for the section show essentially the same feature—the greatest variations occur at very low Reynolds Numbers. Typical full scale Reynolds Num­bers for aircraft in flight may be 3 to 500 million where the boundary layer is predominately turbulent. Scale model tests may involve Reynolds Numbers of 0.1 to 5 million where the boundary layer be predominately laminar. Hence, the “scale” corrections are very neces­sary to correlate the principal aerodynamic characteristics.

The very large changes in aerodynamic characteristics at low Reynolds Numbers are due in great part to the low energy laminar boundary layer typical of low Reynolds Num­bers. Low Reynolds Numbers are the result of some combination of low velocity, small

size, and high kinematic viscosity =

Thus, small surfaces, low flight speeds, or very high altitudes can provide the regime of low Reynolds Numbers. One interesting phenom­enon associated with low RN is the high form drag due to separation of the low energy boundary layer. The ordinary golf ball oper­ates at low RN and would have very high form drag without dimpling. The surface roughness from dimpling disturbs the laminar boundary layer forcing a premature transition to turbulent. The forced turbulence in the boundary layer reduces the form drag by pro­viding a higher energy boundary layer to allay separation. Essentially the same effect can be produced on a model airplane wing by roughening the leading edge—the turbulent boundary layer obtained may reduce the form drag due to separation. In each instance, the forced transition will be beneficial if the reduc­tion in form drag is greater than the increase in skin friction. Of course, this possibility exists only at low Reynolds Numbers.

In a similar sense, “trip" wires or small surface protuberances on a wind tunnel model may be used to force transition of the boundary layer and simulate the effect of higher Reynolds Numbers.