Assuming 2-D, steady, inviscid and irrotational compressible flow with uniform conditions at infinity, the governing equations of conservation of mass, the irrotationality condition and energy equation (generalized Bernoulli) read in terms of the perturbation velocity components (u, w) © Springer Science+Business Media Dordrecht 2015
J. J. Chattot and M. M. Hafez, Theoretical and Applied Aerodynamics,
DOI 10.1007/978-94-017-9825-9_4
|
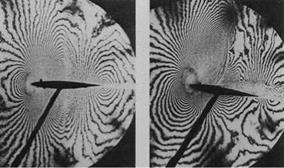
Fig. 4.1 Holographic interferometry of transonic flow fields, (from history. nasa. gov)
|
|
|
dp(U + u) | dpw 0 dx + dz
|
(4.1)
|
|
dw du dx dz ^
|
(4.2)
|
|
Y p V 2
+ = H0 = const. (Y – 1)P 2 0
|
(4.3)
|
|
where y = cr is the ratio of specific heats, ~V = (U + u, w) the total velocity and
cv
Ho is the uniform stagnation enthalpy for isoenergetic flow. The entropy for such flows is uniform and can be written
|
|
p p o
= Y = const.
p1 pY
|
(4.4)
|
|
For air, the gas index is y = 1.4. The subscript “0”
|
stands for undisturbed,
|
incoming flow quantities.
Elimination of pressure between the energy equation and the entropy condition yields a density-velocity relation
|
|
|
|
|
|
|
where the incoming Mach number and speed of sound are M0 respectively.
|
|
|
|
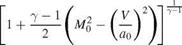
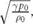

![]()
![]()











