INTERPRETATION OF HIGH-ORDER SYSTEM AS A CHAIN

The transfer function for any selected input/output pair can be found as an element of G given by (3.2,23), i. e.

G = B-!C

where В = si — A, as in Sec. 3.3 and A and C are the constant matrices that define the system. In view of the definition of the inverse matrix we see that G is given by

G = C (3.4,1)

№

where/(s) is the characteristic polynomial (3.3,7). As already pointed out in Sec. 3.3 the elements of adj В are also polynomials in s. It follows from (3.4,1) and (3.3,7) that each element of G is of the form

_________ Щ*)________

(« – *l)(« -*,)•••(«- К)

where N(s) is some polynomial. Now some of the eigenvalues Xr are real, but others occur in complex pairs, so to obtain a product of factors containing only real numbers we rewrite the denominator thus

m 14(n+m)

/(«) = П(«- K) IT (s2 + ars + br) (3.4,3)

r—1 r=m+1

Here Xr are the m real roots off (s) and the quadratic factors with real co­efficients ar and br produce the (n — m) complex roots. It is then clearly

evident that the transfer function (3.4,2) is also the overall transfer function of the fictitious system made up of the series of elements shown in Fig. 3.8. The leading component N(s) is of course particular to the system, but all the remaining ones are of one or other of two simple kinds. These two, first-order components and second-order components, may therefore he regarded as the basic building blocks of linear/invariant systems. It is for this reason that it is important to understand their characteristics well—the

m first-order 1/2 (n – m) second-order components components Fig. 3.8 High-order system as a “chain.”

properties of all higher-order systems can be inferred directly from those of these two basic elements.

IMPULSE RESPONSE

The system is specified to he initially quiescent and at time zero is sub­jected to a single impulsive input

*,(<) = Щ (3.4,4)

The Laplace transform of the ith component of the output is then

Vi(s) = Gu(s) $(s)

which, from Table 2.3, item 1, becomes

Vi(s) = Gds)

This response to the unit impulse is called the impulsive admittance and is denoted Лг7(/). It follows that

M«) = Gu(s) («)

i. e. G(s) is the Laplace transform of h(t)

w <3-4’5)

From the inversion theorem, (2.3,8) is then given by hi(t) = fG{j(s)estds

27n Jc

Now if the system is stable, all the poles of Gtj(s) lie in the left half of the s plane, and this is the usual case of interest. The line integral of (3.4,6) can then be taken on the imaginary axis, s = ico, so that (3.4,6) leads to

1 f00

*«(*) = ;r e’at°o(^) dm 2iTT J—oo

i. e. it is the inverse Fourier transform of G{j(ico). The significance of Gu(ico) will be seen later.

For a first-order component with eigenvalue A the differential equation is

у — Xy = x (3.4,8)

for which we easily get

G(s) = h(s) = —(3.4,9) s — A

The inverse is found directly from item 8 of Table 2.3 as

h{t) = eu

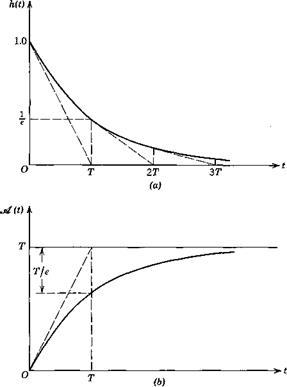
For convenience in interpretation, A is frequently written as A = —1/77, where T is termed the time constant of the system. Then

h(t) = e~tlT

A graph of h(t) is presented in Fig. 3.9a, and shows clearly the significance of the time constant T.

For a second-order system the differential equation is (2.4,1) from which it easily follows that

(3.4,11)

Let the eigenvalues be A = n 4: ico, (cf. 2.5,2) where

n =

_ со = <ып( 1 — £,2)Vz

then h(s) becomes

h(s) =—————————————-

(s — n — ico)(s — n + ico)

– 1

(•s2 — n2) + ft)2

and the inverse is found from item 13, Table 3.3 to be

CO

Fig. 3.9 Admittances of a first-order system.

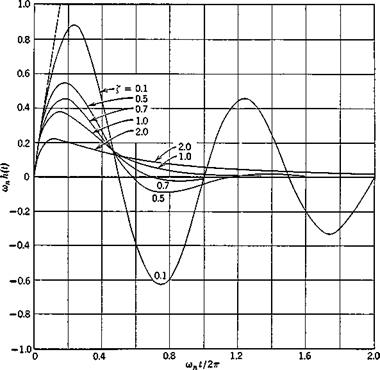
For a stable system n is negative and (3.4,12) describes a damped sinusoid of frequency cc. This is plotted for various £ in Fig. 3.10. Note that the coordinates are so chosen as to lead to a one-parameter family of curves. Actually the above result only applies for £ <: 1. The corresponding ex­pression for £ ;> 1 is easily found by the same method and is

h(t) = ~ ent sinh oj’t (3.4,13)

со

where

m’ = ft>„(£2 – l)1^

Graphs of (3.4,13) are also included in Fig. 3.10, although in this case the second-order representation could be replaced by two first-order elements in

Fie. 3.10 Impulsive admittance of second-order systems.