Lift and Drag

The aerodynamic force Fad can be resolved into two component forces, one at right angles to V and the other opposite to V, as shown in Figure 1.1. The force component normal to V is called lift L and the

Theoretical Aerodynamics, First Edition. Ethirajan Rathakrishnan.

© 2013 John Wiley & Sons Singapore Pte. Ltd. Published 2013 by John Wiley & Sons Singapore Pte. Ltd.

component opposite to V is called drag D. If в is the angle between L and Fad, we have:

Fad cos в

Fad sin в D

T’

The angle в is called the glide angle. For keeping the drag at low value, the gliding angle has to be small. An aircraft with a small gliding angle is said to be streamlined.

At this stage, it is essential to realize that the lift and drag are related to vertical and horizontal directions. To fix this idea, the lift and drag are formally defined as follows:

“Lift is the component of the aerodynamic force perpendicular to the direction of motion."

“Drag is the component of the aerodynamic force opposite to the direction of motion."

Note: It is important to understand the physical meaning of the statement, “an aircraft with a small gliding angle в is said to be streamlined.” This explicitly implies that when в is large the aircraft can not be regarded as a streamlined body. This may make us wonder about the nature of the aircraft geometry, whether it is streamlined or bluff. In our basic courses, we learned that all high-speed vehicles are streamlined bodies. According to this concept, an aircraft should be a streamlined body. But at large в it can not be declared as a streamlined body. What is the genesis for this drastic conflict? These doubts will be cleared if we get the correct meaning of the bluff and streamlined geometries. In fluid dynamics, we learn that:

“a streamlined body is that for which the skin friction drag accounts for the major portion of the total drag, and the wake drag is very small."

“A bluff body is that for which the wake drag accounts for the major portion of the total drag, and the skin friction drag is insignificant."

Therefore, the basis for declaring a body as streamlined or bluff is the relative magnitudes of skin friction and wake drag components and not just the geometry of the body shape alone. Indeed, sometimes the shape of the body can be misleading in this issue. For instance, a thin flat plate kept parallel to the flow, as shown is Figure 1.2(a), is a perfectly streamlined body, but the same plate kept normal to the flow, as shown is Figure 1.2(b), is a typical bluff body. This clearly demonstrates that the streamlined and bluff nature of a body is dictated by the combined effect of the body geometry and its orientation to the flow direction. Therefore, even though an aircraft is usually regarded as a streamlined body, it can behave as a bluff body when the gliding angle в is large, causing the formation of large wake, leading to a large value of wake drag. That is why it is stated that, “for small values of gliding angle в an aircraft is said

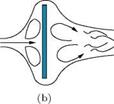Figure 1.2 A flat plate (a) parallel to the flow, (b) normal to the flow.

to be streamlined.” Also, it is essential to realize that all commercial aircraft are usually operated with small gliding angle in most portion of their mission and hence are referred to as streamlined bodies. All fighter aircraft, on the other hand, are designed for maneuvers such as free fall, pull out and pull up, during which they behave as bluff bodies.

Example 1.1

An aircraft of mass 1500 kg is in steady level flight. If the wing incidence with respect to the freestream flow is 3°, determine the lift to drag ratio of the aircraft.

Solution

Given, m = 1500 kg and в = 3°.

In level flight the weight of the aircraft is supported by the lift. Therefore, the lift is:

L = W = mg = 1500 x 9.81 = 14715 N.

The relation between the aerodynamic force, Fad, and lift, L, is:

L = Fad cos в.

The aerodynamic force becomes:

L

Fad =

cos в _ 14715 cos 3°

= 14735.2 N.

The relation between the aerodynamic force, Fad, and drag, D, is:

D = Fad sin в.

Therefore, the drag becomes:

L 14715

D

Note: The lift to drag ratio L/D is termed aerodynamic efficiency.