Momentum Analysis in Forward Flight

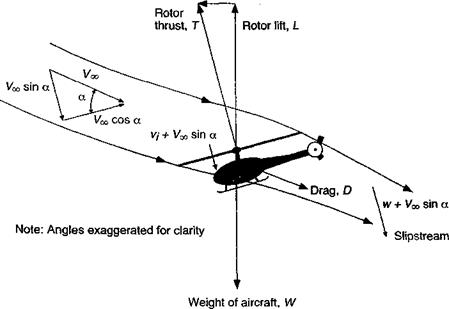
Under forward flight conditions the rotor moves through the air with an edgewise component of velocity that is parallel to the plane of the rotor disk. Because helicopter rotors are required to produce both a lifting-force (to overcome the weight of the helicopter) and a propulsive force (to propel the helicopter forward), the rotor disk must be tilted forward at an AoA relative to the oncoming flow. Under these conditions the axisymmetry of the flow through the rotor is lost. Despite the inherently more complicated nature of the rotor flow in forward flight, the simple momentum theory can be extended to encompass these conditions on the basis of certain assumptions.

The following treatment of rotor performance in forward flight was first derived by Glauert (1928, 1935). An adaptation of Glauert’s flow model is shown in Fig. 2.23, where the analysis is performed with respect to an axis aligned with the rotor disk. The mass flow rate, m, through the actuator disk is now

/’■ч 1

*Z. l VI)

Propulsive force Figure 2.23 Glauert’s flow model for the momentum analysis of a rotor in forward flight.

where U is the resultant velocity at the disk and is given by

U = yj(Voo cos a)2 + (Voo sin a + u, )2 = д/v^ + IVooVi sin a + vf. (2.108)

Glauert makes note that there is no rigor in this assumption for the resultant velocity other than it allows the forward flight theory to reduce to the correct limits in hovering and forward flight – a point also noted by Squire (1948). The application of the conservation of momentum in a direction normal to the disk gives

T = m(w + Vqo sin a) — m V^ sin a = mw (2.109)

and by the application of conservation of energy, we obtain

P = T(t’i + Vqo sin a) = – jrii{Voo sin a + w)2 — sin2 a

= – m (IVqqW sin a + w2).

Using Eqs. 2.109 and 2.110 we get

2wvi + 2Vqo w sin a = 2VoqW sin a + w2

or simply w = 2Vi, which is the same result shown previously for the axial flight cases. Therefore,

T = 2mvi = 2pAUvi — 2pAviyjV^0 + 2VooVi sina + vf. (2.112)

Notice that for hovering flight, Voo = 0, so that Eq. 2.112 reduces to

T = 2 pAvf = 2 pAv2, (2.113)

which confirms that the forward flight result above reduces to the hover result (Eq. 2.14), as required. As forward flight speed increases such that Voo u;, then Eq. 2.112 reduces to

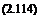T = 2 pAviV0

which is called Glauert’s “high-speed” approximation. This latter result is exactly the lift on an elliptically loaded fixed-wing with a circular planform of radius R, and it should be expected that the results of the momentum theory analysis of the rotor in high-speed forward flight (excluding stall and reverse flow) should agree with fixed-wing theories (see Question 2.16). This is because the rotational speed of the rotor becomes a relatively smaller part of the forward flight velocity and the rotor must act more and more like a regular wing. This can be shown starting from the elliptical form of the spanwise circulation, Г, on the wing, that is,

гО) = Го^І – (|)2, (2.115)

where Го is the circulation at mid-span (y — 0). By using the transformation у = —R cos в this result can be written simply as

Г($) = Го sin 0.

The total lift on the wing can be obtained by integration using

T = L=pVxj r(y)dy = pVccR J rmsmede = pVOQr0R(~y

(2.117)

For an elliptically loaded wing of eliptical planform then the induced downwash u(- is constant across the span and is related to Го by

Го

4 R

Rearranging and substituting in Eq. 2.117 gives the lift as

L = T = pVooR (|) (4Rvd = IpV^ViinR1) = 2pAv, Vx, (2.119)

which is exactly the result in Eq. 2.114. See also Ormiston (2004) for a more detailed discussion of such equivalent wing concepts and their limitations.

2.14.1 Induced Velocity in Forward Flight

In forward flight, it has been shown in Eq. 2.112 that the rotor thrust is given by T = 2m Vi = 2(pAU)Vi (2.120)

or

T = 2pAviy/(VOQ cos a)2 + (V^ sin a + v,-)2.

Recall from Eq. 2.113 that for hovering flight v = T/2pA, then the induced velocity in forward flight can be written as

Vh

«I = – г……………. , * (2.122)

v (Voo cos a)2 + (Voo sin a + Vi)2

The idea of a tip speed ratio or advance ratio, pt, is now used. By using the velocity parallel to the plane of the rotor, then we define gt = cos a/£2R. The inflow ratio is

A = (Vqo sin a + v^/ QR. This leads to the expression

Voo sin OC Vi

A =—————- 1—— = її tan a + A,-

QRQR

But, it is also known from the hover case that А/, = л/Ст/2, therefore,

Cj

A; = —L… . .

2y/ pi2 + A2

Finally, the solution for the inflow ratio, A, is

A = /rtanaH——– — ——- . (2.126)

27^ + 12

While analytic solutions to this equation can be found, in practice a simple numerical procedure is usually used to solve for A.