Numerical Argorithm

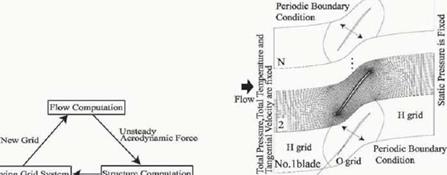
A numerical fl>w-structure coupled method has been developed in the course of the present study [5]. Figure 1 shows the procedure of the method. The com­puted unsteady aerodynamic force in the flow calculation is introduced into the structural calculation in which the equation of motion of the blade is solved to obtain the blade displacement. The computed blade displacement is used for generation of the new grid coordinates in the next time step of fl>w calculation.

The fl>w calculation is based on the two-dimensional nonlinear Euler equa­tion, that is solved through a second order upwind TVD scheme. LU-ADI

factorization algorithm coupled with Newtonian iterations is used as the time – marching scheme. Figure 2 shows computational domain, grid, and boundary conditions. The number of fbw channel, N, can be arbitrarily selected in the computation, and the inter blade phase angles of 360n/N (n=’l,2, …, N) can exist in N fbw channels. Periodic boundary conditions were imposed on the upper and lower side of the computational domain, that is, physical values at the lower boundary of No. 1 fbw region and those at upper boundary of No. N fbw region were set to be same. At the inlet boundary, total pressure, total tem­perature, and rotational speed (tangential velocity) were fixed. Non-refbcting boundary condition was used on the inlet boundary to prevent refection of the wave induced by the blade vibration. Static pressure was specified at the outlet boundary, and the blade surfaces were treated as slip boundaries. H+O+H grid was adopted for computation. О grid was used around the blades to achieve good orthogonality, and H-grids were generated in upstream and downstream regions in order to make inlet and outlet boundaries distant from the blades.

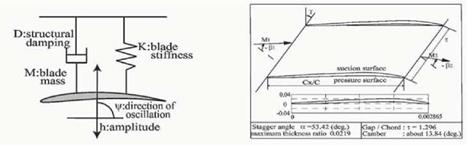
Figure 3 shows structural model of blades in one-degree of freedom. The direction of blade movement, indicated by the angle Ф in Fig.3, can be arbi­trarily selected. The equation of motion of structural model as shown in Fig.3 is written by the following equation (I);

(I)

where M is blade mass, h is blade displacement, D is structural damping, К is blade stiffness, and L is unsteady aerodynamic force acted on blade. This equation was solved through Runge-Kutta-Gill scheme. The structural

Figure 4. Cascade Model (Tip Section of Quiet Fan B)

damping, D, was neglected in the present analysis to concentrate our focus on the aerodynamic damping effect in the fbw-structure coupled situation.