Numerical Solution of the Fundamental Integral Equation

Numerical solution of the fundamental integral equation can be obtained cheaply and accurately for arbitrary geometries. Such simulation tools replace advantageously the analytical method and allow to spend more time analyzing the results and understand­ing the physics, than computing integrals. The benefit of the theory is undeniable in demonstrating the dependency of lift and moment on solely a few modes and in helping understand the suction force and the notion of ideal angle of attack. The fundamental integral equation of thin airfoil theory

w(x, 0) = — —Цd£ = U(d'(x) – a (3.117)

2W0 x – £

is solved using finite differences. One important feature in the discretization of the problem is the use of the Glauert transformation, which allows for rapid convergence and high accuracy. Let the distribution of control points be given by

This very large, practically full matrix, can be solved efficiently by relaxation as

ІХ

ai, i АГ = U (f’ – a) – £ ai, j Гп, п+1, i = 2, 3,…,ix – 1 (3.124)

j =2

(3.125)

and Г”+1 = Г" +шАГі. n represent the iteration index and the upper index (n, n +1) indicates that the value may be “old” or “new”. The relaxation factor [4], 0 < w < 2, can be chosen as high as w = 1.8.

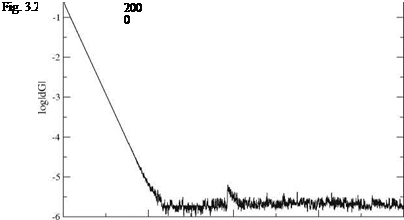
The convergence history with a fine mesh of ix = 101 points is shown in Fig. 3.27. It takes about 500 iterations to converge to machine accuracy.

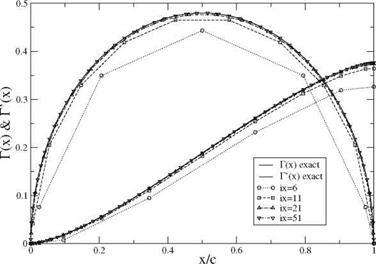
Results for the parabolic plate at zero incidence are presented in Fig.3.28 and compared with the analytic solution for mesh systems of ix = 6, 11, 21 and 51 points. As can be seen, results are sufficiently accurate with ix > 21.

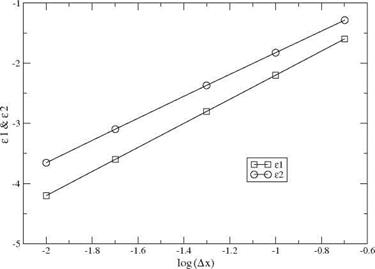
The convergence with mesh refinement is shown in Fig. 3.29, where the following error norms have been used

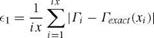
(3.126)

Fig. 3.28 Comparison with analytic solution of Г and Г’

Fig. 3.29 Rate of convergence of Г and Г

The circulation Г converges with a slope of 2. The rate of convergence of 1.8 for Г’ is slightly less, probably due to the singularity in slope at x = 0 and x = c.