Qualitative Behavior of the Radiation-Adiabatic Temperature on Real Configurations

In the design of hypersonic flight vehicles the qualitative behavior of the radiation-adiabatic temperature on more or less flat surface portions is not the only interesting aspect. The behavior at the vehicle nose and at the lead­ing edges is of particular interest, because on the one hand the boundary layer is very thin in the stagnation-point region and along attachment lines,
and on the other hand nose and leading-edge radii, and leading-edge sweep govern the wave drag of a vehicle.[21]

We consider only the proportionality T/a ж 1/5, and that the boundary – layer thickness 5 is inversely proportional to the square root of the flow ac­celeration (5 ос 1 / pdue/dx, x along the respective surface), Sub-Section 7.2.2. The acceleration due/dx in turn is inversely proportional to the nose or leading-edge radius R, Sub-Section 6.7.2. These observations approximately give the general trends shown in Table 3.1.

Not surprisingly the fourth power of the radiation-adiabatic temperature is, like the cold-wall heat flux, inversely proportional to the square root of the nose radius [9], and decreases at a leading edge with increasing sweep. Thick boundary layers, which occur at stagnation areas with large radii, and at leading edges with large sweep (and large radius), lead to large efficiency of surface radiation cooling. This is, with regard to thermal loads, the phe­nomenon, which leads to the blunt shapes of RV’s.

The result for swept leading edges needs a closer inspection. Actually it reflects the behavior of the attachment-line boundary layer. Accordingly it must be generalized, because primary attachment lines move at slender configurations with increasing angle of attack away from the leading edge towards the lower (windward) side of the configuration.[22] Secondary and even tertiary attachment lines occur at the leeward side of a configuration at large angle of attack, together with separation lines [18].

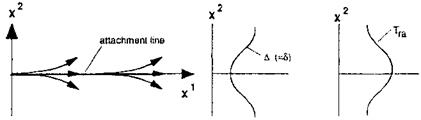
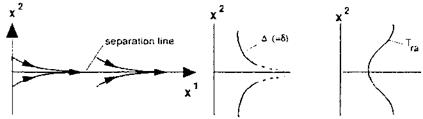
What happens at such lines? At an attachment line, due to the diverging flow pattern, the boundary layer is thinner than that in the vicinity [18], Fig. 3.5. At a separation line, the flow has a converging pattern and hence the tendency is the other way around, Fig. 3.6.

Consequently the characteristic boundary-layer thickness A is reduced at attachment lines, and one has to expect there a rise of the radiation-adiabatic temperature compared to that in the vicinity. Indeed, as will be shown in Section 3.3, a hot-spot situation arises at attachment lines (attachment-line heating), whereas at separation lines the opposite happens, i. e., a cold-spot situation ensues. Attachment-line heating was observed during the first flights of the Space Shuttle Orbiter at the orbital maneuvering system (OMS) pod, and at that time was dubbed “vortex scrubbing”, probably because the re­spective attachment line was changing its location with flight attitude and speed [4]. The A-behavior can be observed in three-dimensional boundary – layer calculations, [18], see also Sub-Section 7.2.1. Finally it is emphasized, that attachment-line heating, like attachment-line laminar-turbulent transi­tion (see Section 8), is connected not only to leading edges, but to the topol­ogy of the skin-friction field of the entire flow-field under consideration.[23]