RELATION BETWEEN IMPULSE RESPONSE AND AUTONOMOUS SOLUTION

It follows from (3.4,5a) that the matrix of impulse response functions H = [7i. w] is related to that of the transfer functions by

H(s) = G(s) (3.4,14)

Furthermore, from (3.2,23) we have that G(s) = B_1(s)C, so that

H(s) = B-!(s)C (3.4,15)

or B-!(s) = ЇВДС-1 (3.4,16)

Now in the autonomous case we have (3.3,4)

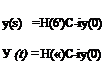Substitution of (3.4,16) into (3.3,4) yields the result for the autonomous solution with initial condition y(0), i. e.

STEP-FUNCTION RESPONSE

This is like the impulse response treated above except that the input is the unit step function 1(1), with transform 1/s. The response in this case is called the indicial admittance, and is denoted It follows then that

	= адї(«) = — s	(a)	(3.4,18)
or		(b)

Since the initial values (at t = 0~) of hi}(t) and are both zero, the

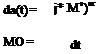theorem (2.3,16) shows that

Thus can be found either by direct inversion of (3.4,186) (see examples

in Sec. 2.5) or by integration of By either method the results for first – and second-order systems are readily obtained, and are as follows (for a single input/output pair the indicial subscript is dropped) :

First-order system:

s/(t) = T( 1 – e~t/T) (3.4,20)

Second-order system:

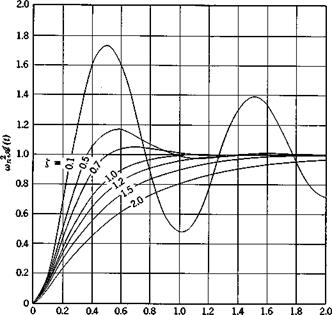
1 — en<(eos cot — — sin a)t)l, £ < 1 (3.4,21)

со J

and for £ > 1, s/(t) is given by the r. h.s. of (2.5,5).

Graphs of the indicial responses are given in Figs. 3.96 and 3.11.

o>nt/2w Fig. 3.11 Indicial admittance of second-order systems.