Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
RESPONSE OF LINEAR/INVARIANT SYSTEMS
As remarked in Sec. 3.2, one of the basic problems of system analysis is that of calculating the system output for a given input, i. e. its response. This is the problem of nonautonomous performance, in contrast with the
|
|
|
(1)
|
|
(2)
|
|
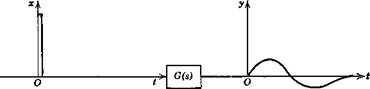
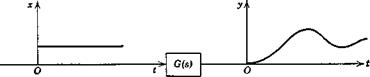
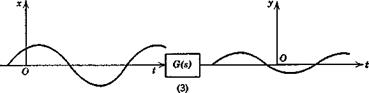
Fig. 3.7 The four basic response problems. (1) Impulse response. (2) Step response. (3) Frequency response. (4) Response to random input. |
autonomous behavior treated in the preceding section. The former is associated with nonzero inputs and zero initial conditions, whereas the reverse holds for the latter.
It is evident that the transfer function defined in Sec. 3.2 supplies all that is required for such response calculations—and provided that the input and transfer function are not too complicated, the whole procedure can be carried out analytically, leading to closed-form results. The method, of course, is to calculate the Laplace transform of the input, and then carry out the inverse transformation of y(s) = 0(s)x(s). When this is not practical, it is necessary to resort to machine computation to get answers.
The major response properties of linear/invariant systems can be displayed by considering four basic kinds of input, as illustrated in Fig. 3.7. These are treated individually in the sections that follow. Before proceeding to them, however, we shall first digress to consider a useful interpretation of the transfer functions of high-order systems.
