Shock Waves and Wave Drag

The normal shock wave shown in Figure 8.6 will typically result in shock losses and associated wave drag which are important in transonic flows. From conservation of mass, momentum, and total enthalpy across a normal shock wave, the total pressure ratio across the shock is calculated to be

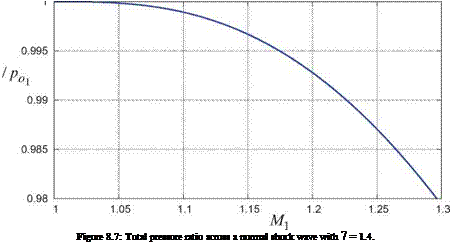where M1 and po1 are just upstream of the shock, and p02 is just downstream. This ratio is plotted in Figure 8.7. The second approximate form in (8.13) is based on an asymptotic analysis of the exact form for M1 ^ 1. It shows that the total pressure loss is cubic in M1 — 1, with the “knee” roughly at M1 ~ 1.15 beyond which the loss increases rapidly.

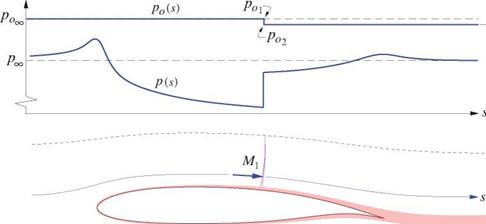
The streamlines passing through the shock suffer a reduction in total pressure, from p0l = p0ix down to p02 = P0wake which persists downstream, as shown in Figure 8.8. When they reach ambient pressure pTO downstream, they will therefore have a velocity below freestream VWake < VL>, and thus form a shock wake.

hwake (A

shock defect (wave drag)

viscous defect (profile drag)

To quantify the magnitude of this shock wake defect we first write the total pressure in terms of the static pressure and the velocity.

Applying this to the shock wake we set p = and p0 = p0 k = p0ixi (p02 /p0l), which then gives the

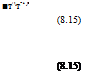shock-wake velocity for any given streamline.

Here Mi is the shock-wave Mach number which that streamline had just before passing though the shock, as shown in Figure 8.8. The final simplified form (8.17) assumes і — VWake/VL ^ і which holds for any practical transonic flow. This wake velocity ratio is plotted in Figure 8.9 for two freestream Mach numbers.

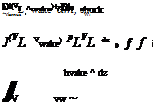Total section drag/span is the total momentum defect of the wake shown in Figure 8.8. The wave drag is the part corresponding to the mass flow which passed through the shock, with the remainder being the usual viscous defect.

The approximations above assume that the wake defect is small compared to unity, which is quite reasonable.

Since typical transonic airfoils have cd ~ 0.0і or less, and the shock height and corresponding shock wake height is a significant fraction of the chord length, it is clear that the fractional defect і — VWake/VL must be kept well below roughly 0.01 to keep Cdwave from adding significantly to the total drag. Hence, a relatively weak shock of M1 < і.2 or less is required for acceptably low wave drag of transonic airfoils.