Slender Body Aerodynamics

Munk-Jones airship theory is a good old useful tool for analyzing the aerodynamic behavior of slender bodies at small angles of attack even at supersonic speeds. The cross flow of a slender wing at a small angle of attack is approximately incompressible. Therefore, according to the Newton’s second law of motion, during the vertical motion of a slender body, the vertical momentum change of the air parcel with constant density displaced by the body motion is equal to the dif­ferential force acting on the body. Using this relation, we can decide on the aerodynamic stability of the slender body if we examine the sign of the

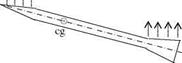
Fig. 1.7 Vertical forces act­ing on the slender body at angle of attack a

aerodynamic moment about the center of gravity of the body. Expressing the change of the vertical force L, as a lifting force in terms of the cross sectional are S and the equation of the axis z = za(x) of the body we obtain the following relation

In Fig. 1.7, shown are the vertical forces affecting the slender body whose axis is at an angle of attack a with the free stream direction. Note that the vertical forces are non zero only at the nose and at the tail area because of the cross sectional area increase in those regions. Since there is no area change along the middle portion of the body, there is no vertical force generated at that portion of the body.

As we see in Fig. 1.7, the change of the moment with angle of attack taken around the center of gravity determines the stability of the body. The net moment of the forces acting at the nose and at the tail of the body counteracts with each other to give the sign of the total moment change with a. The area increase at the tail section contributes to the stability as opposed to the apparent area increase at the nose region.