Some Parametric Considerations of the Radiation-Adiabatic Temperature

We consider finally some general properties of the radiation-adiabatic tem­perature. This done in a very generic way. Neither configurational nor high – temperature real-gas effects are taken into account.

We take eq. (3.25), set for convenience T’2Щ-1 = 1, assume Tra ^ Tr, and write it for Tra in terms only of the emissivity coefficient є, the unit Reynolds number Reu, and the recovery temperature Tr

Tra = C є-0-25^еи)0-25(1-п) T025, (3.36)

with n = 0.5 for laminar flow, and n = 0.2 for turbulent flow.

Assuming further large flight Mach numbers M, we arrive at

Tra = C є-0-25 (Reu)0-25(1-M M0-5. (3.37)

The total differential of Tra has the following terms:

-0.25 Єє-1’25 (Reu)0’25(1-n) M0’5,

Єє-0’25 0.25 (1 – n) (Reu)-(0’75+0’25n) M0’5,

C є-0’25 (Reu)0’25(1-п) 0.5 M-0’5

For the discussion of these terms we generate a few quantitative data. We chose the trajectory points H = 60.56 km (point 1, laminar flow) and H = 36.4 km (point 2, turbulent flow) from Fig. 3.3 and consider the location x/L = 0.5 on the lower symmetry line, Table 3.4.

For the two points the respective constants C are determined (note that they have a secondary influence on the slopes of the curves) and the functions Tra of є, Fig. 3.12, ReZ^, Fig. 3.13, and MTO, Fig. 3.14 are found. They are valid in the vicinity of the two points (full lines in the figures). Away from the points they indicate only the trend (broken lines).

We obtain the following results:

Table 3.4. Selected flight parameters (Fig. 3.3) of the Space Shuttle Orbiter [22, 23]. Point Moo H [km] Relo [1/m] Too [K] Tra [K] at = 0.5 Boundary layer 1 15.7 60.56 7.64-104 253 960 laminar 2 5.22 36.4 7.99-105 222 860 turbulent

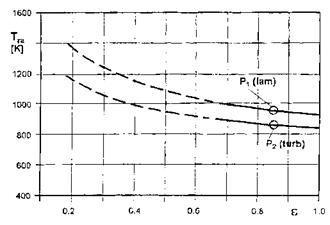
— Tra depends inversely on є0-25 and hence decreases with increasing є, Fig. 3.12, for both laminar (high altitude) and turbulent (low altitude) flow.

Fig. 3.12. Parametric considerations: Tra at x/L = 0.5 along the lower symmetry line of the Space Shuttle Orbiter as function of the emissivity coefficient є around point 1 (laminar flow) and point 2 (turbulent flow) (see Table 3.4). Full lines: range of validity of the approximation, broken lines: trend extrapolation.

The gradient дТга/дє also decreases with increasing є, eq. (3.38). At large є we find the important result (be careful with the generalization of this result!) that Tra becomes insensitive to changes of є. At є = 0.85 т 0.05, for instance, we find only ATra 10 K at both trajectory points.

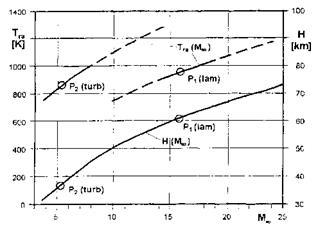
— The dependence of Tra on ReU is more complex. Tra increases in any case strongly with increasing Re^, Fig. 3.13, and slightly stronger for turbulent than for laminar flow, reflecting the dependence of the respective charac­teristic boundary-layer thicknesses on the Reynolds number. The gradient dTra/dReu decreases with increasing Reu, eq. (3.39), stronger for laminar than for turbulent flow (note that in Fig. 3.13 not the true dependence on Reu but on Reu(H) is given).

— With increasing M^ we get the expected growth of Tra, Fig. 3.13. The gradient dTra/dM decreases with increasing M, eq. (3.40). The different

Fig. 3.13. Parametric considerations: Tra at x/L = 0.5 along the lower symmetry line of the Space Shuttle Orbiter as function of the unit Reynolds number Re^ around point 1 (laminar flow) and point 2 (turbulent flow) (see Table 3.4). Full lines: range of validity of the approximation, broken lines: trend extrapolation, H(Reж) is exact.

slopes of the curves are due to the different magnitudes of the constant C in point 1 and 2 (note that in Fig. 3.14 Tra is given as a function of M(H) and not of M).

Fig. 3.14. Parametric considerations: Tra at x/L = 0.5 on the lower symmetry line of the Space Shuttle Orbiter as function of the Mach number Мж around point 1 (laminar flow) and point 2 (turbulent flow) (see Table 3.4). Full lines: range of validity of the approximation, broken lines: trend extrapolation, H(Мж) is exact.