The conservation of momentum

Conservation of momentum requires that the time rate of change of momentum in a given direction is equal to the sum of the forces acting in that direction. This is known as Newton’s second law of motion and in the model used here the forces concerned are gravitational (body) forces and the surface forces.

Consider a fluid in steady flow, and take any small stream tube as in Fig. 2.4. s is the distance measured along the axis of the stream tube from some arbitrary origin. A is the cross-sectional area of the stream tube at distance s from the arbitrary origin.

p, p, and v represent pressure, density and flow speed respectively.

A, p, p, and v vary with s, i. e. with position along the stream tube, but not with time since the motion is steady.

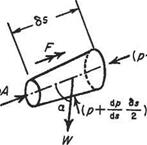
Now consider the small element of fluid shown in Fig. 2.5, which is immersed in fluid of varying pressure. The element is the right frustrum of a cone of length 6s, area A at the upstream section, area A + 6A on the downstream section. The pressure acting on one face of the element is p, and on the other face is p + (dp/ds)6s. Around
78s) (-4+8/1)

Fig. 2.5 The forces on the element

the curved surface the pressure may be taken to be the mean value p + (dp/ds)6s. In addition the weight W of the fluid in the element acts vertically as shown. Shear forces on the surface due to viscosity would add another force, which is ignored here.

As a result of these pressures and the weight, there is a resultant force F acting along the axis of the cylinder where F is given by

where a is the angle between the axis of the stream tube and the vertical.

From Eqn (2.5) it is seen that on neglecting quantities of small order such as (dpjds)6s6A and cancelling,

F = —^f~A 6s — pg A (6s) cos a

since the gravitational force on the fluid in the element is pg A 6s, i. e. volume x density x g.

Now, Newton’s second law of motion (force = mass x acceleration) applied to the element of Fig. 2.5, gives

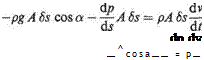(2.7)

where t represents time. Dividing by A 6s this becomes