The Control Hinge Moment

To rotate any of the aerodynamic control surfaces, elevator, aileron, or rudder, about its hinge, it is necessary to apply a force to it to overcome the aerodynamic pressures that resist the motion. This force may be supplied entirely by a human pilot through a mechanical system of cables, pulleys, rods, and levers; it may be provided partly by a powered actuator; or the pilot may be altogether mechanically disconnected from the control surface (“fly-by-wire” or “fly-by-light”). In any case, the force that has to be applied to the control surface must be known with precision if the control system that connects the primary controls in the cockpit to the aerodynamic surface is to be de­signed correctly. The range of control system options is so great that it is not feasible in this text to present a comprehensive coverage of them. We have therefore limited ourselves in this and the following chapter to some material related to elevator con­trol forces when the human pilot supplies all of the actuation, or when a power assist relieves the pilot of a fixed fraction of the force required. This treatment necessarily begins with a discussion of the aerodynamics; that is, of the aerodynamic hinge mo­ment.

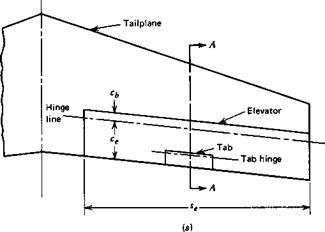
The aerodynamic forces on any control surface produce a moment about the hinge. Figure 2.22 shows a typical tail surface incorporating an elevator with a tab. The tab usually exerts a negligible effect on the lift of the aerodynamic surface to which it is attached, although its influence on the hinge moment is large.

Figure 2.22 Elevator and tab geometry, (a) Plan view. (b) Section A—A.

The coefficient of elevator hinge moment is defined by

He

l2pV2Sece

Here He is the moment, about the elevator hinge line, of the aerodynamic forces on the elevator and tab, Se is the area of that portion of the elevator and tab that lies aft of the elevator hinge line, and ce is a mean chord of the same portion of the elevator and tab. Sometimes ce is taken to be the geometric mean value, that is, ce = SJ2se, and other times it is the root-mean square of ce. The taper of elevators is usually slight, and the difference between the two values is generally small. The reader is cautioned to note which definition is employed when using reports on experimental measure­ments of Che-

Of all the aerodynamic parameters required in stability and control analysis, the hinge-moment coefficients are most difficult to determine with precision. A large number of geometrical parameters influence these coefficients, and the range of de­sign configurations is wide. Scale effects tend to be larger than for many other pa­rameters, owing to the sensitivity of the hinge moment to the state of the boundary layer at the trailing edge. Two-dimensional airfoil theory shows that the hinge mo­ment of simple flap controls is linear with angle of attack and control angle in both subsonic and supersonic flow.

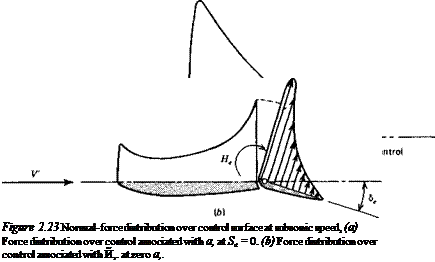
The normal-force distributions typical of subsonic flow associated with changes in a and 8e are shown qualitatively in Fig. 2.23. The force acting on the movable flap has a moment about the hinge that is quite sensitive to its location. Ordinarily the hinge moments in both cases (a) and (b) shown are negative.

In many practical cases it is a satisfactory engineering approximation to assume that for finite surfaces Che is a linear function of as, 8e, and 8r The reader should note however that there are important exceptions in which strong nonlinearities are present.

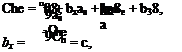We assume therefore that Che is linear, as follows,

a, is the angle of attack of the surface to which the control is attached (wing or tail), and 8, is the angle of deflection of the tab (positive down). The determination of the hinge moment then resolves itself into the determination of b0, bu b2, and b3. The geometrical variables that enter are elevator chord ratio cjc„ balance ratio cjce, nose shape, hinge location, gap, trailing-edge angle, and planform. When a set-back hinge is used, some of the pressure acts ahead of the hinge, and the hinge moment is less than that of a simple flap with a hinge at its leading edge. The force that the control system must exert to hold the elevator at the desired angle is in direct proportion to the hinge moment.

We shall find it convenient subsequently to have an equation like (2.5,1) with a instead of as. For tailless aircraft, a, is equal to a, but for aircraft with tails, as = a,. Let us write for both types

Che ~ Che о + Chea + b2Se + b3S, (2.5,2)

where for tailless aircraft Chen — b0, Chea = bt. For aircraft with tails, the relation be­tween a and a, is derived from (2.3,12) and (2.3,19), that is,

a. S, / де

1——- — (1 – —

a S da

whence it follows that for tailed aircraft, with symmetrical airfoil sections in the tail, for which b0 = 0,