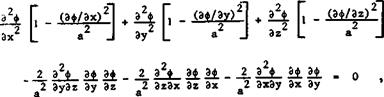THE TREATMENT OF AIRFLOWS

He have already mentioned equations o£ motion which govern the flight of an aircraft and we have seen how much they must be simplified before we can deal with them and derive useful answers. We now want to look at airflows and con­sider models to describe the air (not "the air" itself) and solutions of the equations of motion for gases. Again, the most drastic simplifying assumptions must be made before we can even think about the flow of gases and arrive at equations which are amenable to treatment. Our whole science lives on highly – idealised concepts and ingenious abstractions and approximations. We should remember this in all modesty at all times, especially when sombody claims to have obtained "the right answer" or "the exact solution". At the same time, we must acknowledge and admire the intuitive art of those scientists to whom we owe the many useful concepts and approximations with which we work.

Our aim is to concern ourselves with airflows which have been found useful in engineering applications to aircraft which fly through the earth’s atmosphere at not too high an altitude and not too high a speed. In general, we shall not derive any of the equations nor their solutions. These matters may be found in textbooks, such as those by E Becker (1965), W J Duncan, A S Thom &

A D Young (1970), H Lamb (1932), H W Liepmann & A Roshko (1957), R E Meyer

(1971) , L Prandtl, К Oswatitsch & К Wieghardt (1965), К Oswatitsch (1956),

L Rosenhead (1963), H Schlichting (1960), W R Sears (1955), В Thwaites (1960), A Walz (1969), and К Wieghardt (1965).

2.1 Models to describe the air and some of its properties. We are concerned with air and hence, strictly, with the motion of air molecules. Thus we should start with the kinetic theory of gases, as developed by Boltzmann and Maxwell, which itself already represents a highly-ingenious model of whatever may happen in reality (for some accounts of this theory, which suit our purpose, see e. g. H Grad (1958) and J J Smolderen (1965)). Right from the beginning, we make a severe restriction: the main forms of energy considered are the kinetic energy of molecular translation and the potential energy of molecular inter­action. Next, we assume that the motion of an individual molecule can be re­presented as the combination of a bulk, or macroscopic, component and a random component. Then the kinetic energy is split into two independent terms: the bulk, or gasdynamic, kinetic energy; and the kinetic energy of random motion, i. e. the heat energy. Further, it is assumed that the average distance bet­ween neighbouring particles is always much greater than the molecular radius of interaction, which implies that a gas molecule is subject to interaction forces for only a small part of the time and that there are few collisions between particles. This leads to considerable simplifications in the equations of motion. On the other hand, we assume that there are always enough colli­sions for the gas to remain in a state of equilibrium, on a macroscopic scale, if it is subjected to external disturbances. In other words, the effect of the collisions is simply to redistribute the random energy in such a way that the nature of the molecular interactions cannot be discerned. Without know­ing what happens in between, we can then relate the initial and the final con­ditions of the gas, both being equilibrium conditions.

This behaviour corresponds to the definition of a perfect gas, and the bulk properties of the gas are then described by the Euler equations. In many cases, the transport processes of momentum and heat are of primary interest but, again, the actual molecular interactions which are associated with these processes are not considered in detail but appear only through a set of coefficients for the bulk properties, such as viscosity or thermal conduction. These are characteristically dependent on the temperature of the gas and their values are usually determined by experiments rather than by less reliable computations. The gasdynamic equations then reduce to the Navier – Stokes equations.

It is possible to derive first Boltzmann’s equation, which describes the gas in terms of the motion of its constituent particles, and then from this to derive the Navier-Stokes equations for a fluid. The particle description makes use of a distribution function which defines the velocity and position of a particle at any given time and specifies the number of particles in a given volume. For the concept of a distribution function to be of value, there should be a large number of particles in any volume of physical interest and in any velocity range of physical interest. However, this is already an over-simplification because, in order to describe the motion of a typical molecule completely, we should also specify its angular velocity and, if more precision is required, its vibrational and electronic states as well. Only the simple form leads to Boltzmann’s equation. From it a set of equations of fluid mechanics may be derived. To do this, we make use of the fact that certain properties, such as mass, are conserved in particle collisions. Thus we obtain the equation of continuity in fluid mechanics. In a similar way, we can derive the three components of the momentum equation, since momentum is also conserved in collisions. Finally, we can derive the energy equation, assuming perfectly elastic collisions. In this procedure, various integrals can be identified with various well-known physical properties of the gas, such as the temperature, pressure, heat flux etc.

In deriving the Navier-Stokes equations in this way, a number of additional assumptions are implied: the gas must not be too dense but, on the other hand, there must be a sufficient number of collisions to preserve macroscopic equilibrium. We are, however, fortunate in that these assumptions need not worry us too much because the Navier-Stokes equations, as it happens, give an extremely close approximation to the behaviour of a gas over a much wider range of conditions than are to be expected from the analytical derivation.

One might even say that they are based on experimental observations. They are satisfied by most common liquids, for example, and also by gases with rotational inertia if a suitable choice is made for the ratio of specific heats. Indeed, they have been manipulated almost ad nauseam to take account of vibrational energies, dissociation, ionisation, and electromagnetic effects, although care has to be taken in some of the definitions, particu­larly when departures from equilibrium have to be taken into account. How­ever, for the flight of aircraft to be discussed here, the need for consider­ing these effects will hardly arise.

It should be noted that the set of equations is not closed, in that there are more unknowns than there are equations. The unknown properties are density, pressure, temperature, and the three components of velocity. These must sat­isfy conservation laws of mass, energy, and three components of momentum.

In practice, we fall back on an equation of state, which may also be deduced from kinetic theory, using suitable assumptions, to complete the set. Various attempts to improve on the Navier-Stokes equations have been made, but these have met with only limited success.

We have now arrived at the concept of continuum flows. These may be regarded as a limit in which the number of molecules in a "unit volume" tends to infi­nity and where the typical time and distance between successive collisions for any individual molecule tend to zero by comparison with the "unit time" and "unit length" relevant to the flow problem considered. In continuum flows, the molecular structure of the gas is well hidden.

Having accepted the concept of regarding air to be a continuum, we start to think again in terms of a different kind of air particle, without defining very precisely what we mean by that. We may think of a particle as represen­ting a certain "body of fluid" or a "fluid element". Bulk properties are ac­tually thought of as interactions between such particles, and this is possi­bly the reason why fluid mechanics, and hence aerodynamics, is less an exact and mathematical science than some other disciplines in physics. But that is also the attraction and fascination of fluid mechanics: so many plain and ho­mely problems still wait for a proper solution!

The concept of fluid particles is useful in that it allows us to distinguish the physics of fluid flows from that of solid bodies and of plasticity: fluid particles can easily be moved relative to one another; there is no special initial arrangement of the fluid particles; and small forces are sufficient, and little work needs to be done, to bring about a different arrangement of the particles and to let them flow, if the changes are slow enough. But this is also the reason why it is so difficult to describe and to understand fluid motions.

With this intuitive idea of particles in mind, we can use the concept of den­sity, i. e. the mass per unit volume, to describe how densely packed they are. In gases like air, relatively small forces can change the density and so we consider them to be compressible. If we want to describe the forces and motions within the gas in more detail, we must at least assume that the par­ticles are small enough that any changes of forces and velocities within them can be ignored. Such a particle then experiences only volume forces (like gravity) and forces normal and tangential to its surface. Having simplified matters that far, we are off and away and can begin to write down equations which might give us some useful solutions.

There are several ways in which equations of motion can be written down. One description of the motion which suggests itself is to consider the motion of the fluid particles themselves and to associate it with a geometric trans­formation represented by a function x = x(a, t), giving the position vectors x at various times t of the fluid particle identified by the label a.

This is the Lagrangian description. As it turns out, an explicit considera­tion of the function x(£,t) is rather inconvenient in practice, and there is usually no need for it. For virtually all practical purposes, a description by means of the velocity field, V, considered as a function of x and t is sufficient. This is the Eulerum description, and it is nearly always used.

We may illustrate the Eulerian description by considering the simple idealised case of the flow of an incompressible gas. To think of a gas as being incom­pressible is in itself a bold assumption, but it is often justified in prac­tice. In that case, the function V(x, t) is all we want to know to describe the flow. The equations which govern it can be expected to contain terms which describe the internal forces between the elements within the gas as well as external forces such as field forces and forces exerted by solid boundaries There are pressure forces which act normal to the surface of a fluid particle and also normal to a solid surface. There are also friction forces which act tangential to the surface of a fluid particle and also tangential to a solid surface. These latter forces are supposed to take account of the fact that the medium is viscous. We usually think that internal friction is the greater the greater the relative velocity between fluid particles. The introduction of this concept of friction is based on observations, and we treat like fric­tion forces also those time-average values of exchanges of momentum, that are described as "Reynolds stresses", and which occur when the internal motion of the fluid particles appears to be highly irregular to us in a way which we cannot yet comprehend, and which in our ignorance we cover up with the word turbulent, meaning tumultuous, disorderly, unruly (see e. g. P Bradshaw (1971))

We must also find a consistent postulate for what happens at the interface between a gas and a solid. There, we must go back to the kinetic theory of gases and think in terms of possible reflection processes of the air molecules Real reflection is considered to be a mixture of at least two extreme pro­cesses: specular reflection where the molecules leaving the surface have the same mean tangential velocity as the incident molecules; and diffuse reflec­tion where the molecules leaving the surface have zero mean tangential velo­city. It can then be shown that we must adopt the postulate that the boundary condition at a solid surface is zero relative fluid velocity (see e. g.

R E Meyer (1971) page 83). It may seem peculiar that this boundary condition holds with respect to both the tangential and the normal velocity components. This cannot always be fulfilled in approximate theories, when we do the next steps in introducing simplifying concepts.

One drastic but nevertheless often useful simplification is to ignore the viscosity of the air altogether and, moreover, to assume the flow to be irrotational. In these potential flows, only the condition of zero normal velocity can be fulfilled and tangential slip must be allowed to occur along a solid wall. A more useful simplification which can carry us much further is to assume that all the viscous effects that matter are confined to a thin layer along the surface of the body: Prandtl’s boundary layer. Outside the boundary layer, the flow is taken to be inviscid and irrotational, and the pressure is assumed to be the same throughout the layer as that at a point on the surface underneath. In that flow model, the condition of zero tangential velocity can be fulfilled and account must be taken of the fact that the slowed-down flow near the surface takes up more room and displaces the stream­lines in the external flow outwards, compared with where they would have been had there been no boundary layer. The existence of such a displacement thick­ness means that the flow outside the boundary layer – and hence the pressure along the surface of a given body – is the same as the irrotational flow about a hypothetical body with zero normal velocity, which lies wholly outside the given body (see e. g. M J Lighthill (1958) and К Gersten (1974)). Thus even the boundary conditions to be applied depend on the simplified model of the flow we choose to adopt. In this flow model of Prandtl, work must be done by the body on the boundary layer, as it moves through the air, and momentum is exchanged. Also, the boundary layer air is left behind the body in the form of a wake, and the reduced momentum in the wake corresponds to a drag force on the body.

2.2 Some methods to describe inviscid flows. In many common flow models used in aircraft design, the assumptions are made that the flow is inviscid and that the vorticity is zero everywhere outside the body and its boundary layer and wake. In such flows, the velocity vector V is the gradient of a scalar

function ф, the velocity potential, so that

Vx = Эф/Эх, Vy = Эф/Эу, Vz = Эф/Эг, (2.1)

if we use a rectangular system of coordinates (x, y,z) , where the x-axis is suitably fixed in the body and inclined at an angle a to the direction of the mainstreams which has the velocity Vq. The equation of motion in the Eulerian description then takes the form

where a is the velocity of sound given by

a2 = aQ2 – i(Y – D(VX2 + Vy2 + Vz2 – VQ2) . (2.3)

ag is the velocity of sound in the undisturbed mainstream and thus a constant у is the adiabatic index. Mg = Vg/ag is the Mach number of the mainstream. This description of inviscid continuum flows also implies that energy and entropy are conserved, i. e, the flows are homenergic and ieentropia. Thus the existence of shockwaves in the flowfield is excluded, among other things.

These equations are the basis of many of the design methods we shall discuss. However, we should be clear from the outset that, together with the boundary conditions described above, they are so highly nonlinear that we have not yet succeeded in obtaining solutions for the threedimensional flows we are really interested in. Therefore, we are forced to make further simplifying assump­tions and approximations, on top of all those we have already accepted.

In our attempts to find solutions, we may distinguish between three different approaches:

1 Obtaining accurate numerical solutions of the complete equations.

2 Simplification of the equations.

3 Linearisation of the equations for small perturbations.

Attempts of the first kind have been successful so far only for twodimension­al aerofoils; these will be discussed below in Section 4.3. Some approximate methods for threedimensional wings, to be discussed in Sections 4.3 and 4.5, may give answers of good accuracy, but only for incompressible flows. A method of the second kind, to deal with the effects of compressibility, will be des­cribed in the next Section below. Here, we want to explain procedures of the third kind, which convert the nonlinear equations of motion into linear equa­tions. We illustrate this linearised theory and the many assumptions that it implies by the example of the inviscid flow past a twodimensional aerofoil; its application to threedimensional wings will be taken up in detail in Chap­ters 4, 5, and 6. It may help the understanding to write down the main rela­tions in terms of the velocity components themselves.

Rectangular coordinates (x, z) are fixed in the aerofoil, with x = 0 at the leading edge and x – 1 at the trailing edge. The total velocity V has the components

and

Vz = Vz0 + vz " V0 sin « + vz ’ (2*5>

where Vxq and Vzq are the components of the mainstream and hence constants. The potential equation (2.2) can then be written as a relation for the pertur­bation velocities and takes the form

The boundary conditions are that the velocity tends to that of the mainstream at large distances from the aerofoil and that the velocity component normal to the surface of the aerofoil is zero, which gives a relation between the slope of the aerofoil surface and the velocity components

These equations are still highly nonlinear and we cannot readily solve them analytically, in spite of all the simplifications we have already made, and so there is an incentive to introduce further approximations. These are all based on the assumptions that the perturbations of the mainstream, caused by the aerofoil, are small; that the aerofoil is thin and only slightly cambered, so that the slope of its surface is small; and that the angles of incidence is small. We shall now list, but not defend, the main approximations which are commonly made to arrive at what is called linearised theory. In doing so, we note that the various assumptions are not always consistent; that, in some cases, several assumptions are lumped together;that most of them are accepted only on their plausibility and that no rigorous estimate of the errors intro­duced by them is given. In fact, it has been difficult to write down satis­factorily what the complete sets of first-order and of second-order terms are, and there are cases where a third-order term may matter just as much as the corresponding lower-order terms. For the twodimensional aerofoils considered here, we refer to the work of M J Lighthill (1951), M van Dyke (1955) and

(1964) , and W Gretler (1965). For threedimensional wings, a consistent and practical second-order theory has been provided only recently by J Weber (1972) .

In linearised theory, the main assumptions are as follows: (0 the term (Vx/a)2 in 2 equation (2.6) is replaced by MQ ; 3v V . . 3v (2) the term 2 —- — 3z a Mo is ignored when compared with —£■ 0 z (3) the term <Va)2 is ignored when compared with unity.

With these three assumptions, (2.6) simplifies to

With regard to the boundary condition (2.7), the following assumptions are made:

(4) the term vx is ignored when compared with cos a ;

(5) the velocity component vz(x, zw) on the surface is replaced by the value vz(x,0) on the chordline 2 – 0 ;

(6) the total velocity V(x, zw) on the surface is replaced by the value

V. cos a + v (x,0) on the chordline.

0 x

The boundary condition then reads:

In principle, (2.8) can be solved and the velocity components obtained, with the boundary condition (2.9). Potential theory can be used and a perturbation potential ф introduced, with vx ж Эф/Эх and vz = Эф/Эг, as a convenient way of obtaining actual solutions. The equation to be solved is a form of Laplace’s equation:

+

Эх2

where 8 = (1 – MqM is a constant.

From the velocities we want to derive the pressures acting on the surface. The general relation between the pressures and the velocities in isentropic flow is obtained from Bernoulli’s equation:

where

If the angle of incidence о and the perturbation velocities vx and vz are small, the total velocity can be expanded into a series and the pressure co­efficient can be written as

In fully-linearised theory, we have

For inviscid incompressible flows, the most efficient method of obtaining actual solutions is that of representing the flow by a distribution of singu­larities – sources, doublets, or vortices. This method has been explained in a classical paper by A Betz (1932), and it will be applied many times through­out this book. The singularities are placed either on the surface of the body or inside it and also (for lifting systems) on the vortex wakes behind them. Such distributions of singularities satisfy the equation of motion automatically and also the boundary conditions at infinity. The problem is then reduced to that of satisfying the boundary conditions on the body and the wake. Compared with a so-called field solution, in which the equation of motion is solved explicitly (for example, by a finite-difference method) with the appro­priate boundary conditions, the dimensions of the problem are effectively reduced mathematically by one; and this is essentially the reason for the improved numerical efficiency of such a procedure. It may also be argued that the use of singularities can help the understanding by providing some physical insight. A mathematical source singularity, for example, corresponds exactly to the physical flow model we have in our minds. This should become quite clear when we now consider some simple flows about non-lifting bodies.

A source, or a distribution of sources and sinks, in a stream is a natural flow element in the representation of a displacement flaw, and this is how the flow past bodies of revolution was first treated by W J M Rankine (1871). A single source in a uniform stream produces the flow about a halfbody of semi­infinite length, sometimes called the Blasius-Fuhrmann body, as shown in Fig.

2.1. This displays clearly how the source flow displaces the mainstream

LIVE GRAPH

Click here to view

and generates a streamsurface dividing the air emerging from the source from the mainstream air. This streamsurface may be regarded as the surface of a blunt solid body. The source material is all turned back and fills an area

far downstream with the velocity Vq, so that

Q – |d2Vq (2.15)

in threedimensional flows; and

Q = t V0 (2.16)

in twodimensional flows; where Q is, respectively, the volume of air that emerges from the point source in unit time, or the volume in unit time that emerges from unit (lateral) length of the line source. The velocity field induced by a source alone can readily be determined: for reasons of symmetry, the velocity v is directed along the radius vector _r from the source and it is the same at all points on a sphere – or a circle – with the source

_1 IT 16 2

in threedimensional flows: and

Ir__Lt

V0 " 2" 7

in twodimensional flows. These relations and the example in Fig.2.1 show that the perturbation velocities are much lower in threedimensional flows than in twodimensional flows.

Consider now a non-lifting, symmetrical, aerofoil in an inviscid incompress­ible flow. Such an unswept wing can be represented by a distribution of straight source filaments q(x)dx along the chord c. We now make use of the fact that individual solutions for isolated singularities, which auto­matically fulfil the equation of motion, can be superposed. For a distribution of infinitely long source lines, we find for the velocity component vz normal to the mainstream

v (x,0)

—– = ± і q(x)

which expresses the plausible fact that, at any point, half the source mater­ial is squeezed out upwards and the other half downwards. (2.21) is used as a first approximation for vz on the surface of thin aerofoils, within the context of linearised theory. v? can be related to the shape of the aerofoil if the boundary condition (2.7) is linearised to

	dz(x) _	vz(x)		(2.22)
	dx	о >
i. e. if we assume vx(x, z)	« Vq, as in	(2.9). Hence,
	q(x) =	“oTT1 •		(2.23)
By integration,	z(x) =	2^0/X<l(X,)	dx’	(2.24)
and, in particular,		. 1
	z(0) = z(c) =	Що’ q(x,)	d(x’/c) = 0	»

i. e. the overall strengths of the sources and sinks must be equal in order to obtain a practical aerofoil section which forms a closed contour.

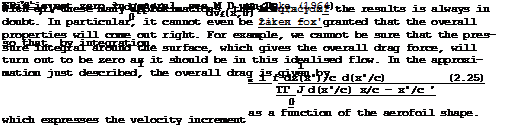With the source distribution being known, the streamwise velocity increment vx can be determined. A single source filament produces on the chordline

These very simple examples will have demonstrated the very many steps we are prepared to take in order to get near a solution. In view of this, it is again and again a matter of wondrous surprise when we find that the answers we obtain in this way bear such a close resemblance to what we observe and that our thinking was not misguided, after all. It may also be said that the linearisation procedure with its underlying concept of small perturbations has made it easier in many ways to think about these flows.

There remains the question of how to obtain actual numerical answers, even in simple cases like (2.25) where only an integration is involved. To explain numerical methods in detail goes beyond the scope of this book, and so we refer only to some of the many valuable accounts of these matters, which have been given recently, such as those by J J Smolderen (1972), P J Roache (1972),

D Rues (1973), E Krause (1973) and (1975), R C Lock (1975) , and M G Hall (1975).

2.3 Some models to describe the compressibility of the air. We may now follow up a little further some of the concepts and approximations we use when dealing with compressible flows. Consider inviscid subsonic flows so that

(2.2) applies.

A very simple method is that of E G Broadbent (1965) who treated a two­dimensional flow (originally, the flow past an electric arc transverse to an airstream), where the assumption could be made that pressure changes may be ignored as compared with density changes and that the streamline pattern is not affected by the Mach number. The equation of motion can then be simpli­fied (case 2 on page 27) and solved to give

V = —L. f (2.27)

which relates the velocity V in compressible flow to the velocity in in­compressible flow. Only the density ratio remains to be determined. A Betz & E Krahn (1949) have derived this relation also for twodimensional flows past solid bodies and found it a useful approximation in the case of a circular cylinder. No method of this kind has been developed for threedimensional flows and we are, therefore, again reduced to methods which are based on the assump­tion that perturbations are small. But these methods have the practical advantage of leading to universal compressibility factors.

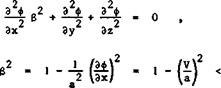For small perturbations, all the mixed terms in (2.2) can be ignored, and only the term (Эф/Эх)2/а2 must be taken into account in the first three terms since it cannot be regarded as small as compared with unity for the high – subsonic flows to be considered. (2.2) then reduces to

for subcritical flows. If we now make yet another drastic assumption and con­sider the value of 8 to be constant, then (2.28) can be reduced to the potential equation for an incompressible flow by the application of the Prandtl-Glauert procedure (see H Glauert (1928), L Prandtl (1936)). For the threedimensional flow past a wing of aspect ratio A = 4s^/S, swept through an angle we transform the wing into an analogous wing (suffix a) by means of

xa =	X
У a =	By
za _	Bz

The streamline analogy of A Busemann (1928) and В GBthert (1941) is applied to wings as explained by D KUchemann & J Weber (1953). The two perturbation potentials are then such that both the real wing and the analogous wing are s treamsurfaces. Thus,

2 2 2

д ф Эф Эф

– 0 , (2.31)

Эх Эу 3z

a J a. a

as required, for an analogous wing which is thinner than the given wing,

t

a

c

and which is more highly swept:

tan фа = і tancp.

Since the lateral dimensions have been reduced according to (2.30), ratio of the analogous wing is also reduced:

Aa = 6 A. (2.34)

From the solution ф of (2.31), the perturbations velocity components v and Vy3 can be derived and these are then related to those of the real wing £y

and

(2.36)

It remains to find a suitable constant value for the parameter 6. The simpl­est approximation is to replace V in (2.29) by the mainstream velocity Vq and the velocity of sound by its value a^ in the mainstream so that

* (2’37)

This is the original "Prandtl-Glauert factor". There have been many attempts to improve on this approximation, and one that has been successful and simple has been proposed by J Weber (1948). This is to replace V in (2.29) by its local value in incompressible flow and again a by ад, so that

This takes at least some account of the fact that the local velocity over the aerofoil is different from the mainstream velocity. In a general way, this approximation is now known as the method of local linearisation, as described by J R Spreiter (1962). Weber’s rule usually gives a better representation of the actual values than the original Prandtl-Glauert rule. The main feature of this procedure is that it circumvents the real problem and reduces the calculation of a compressible flow to that of an incompressible flow. Its implications for swept wings will be discussed further in Section 4.2.

This concept of compressibility factors has proved so powerful that we tend to think in these terms as though they expressed some physical property of these flows. Thus, rather too easily, we tend to regard pressure distributions in compressible flow as scaled-up or stretched versions of those in incompress­ible flow. It is only recently that a practical method for obtaining exact

numerical solutions for twodimensional compressible flows around aerofoils has been developed by С C L Sells (1967). This allows us to determine the error introduced by the approximations, but isolated numerical answers cannot affect our way of thinking about the physics of the flow very much. However, Sells’s pioneer method has proved to be extremely useful and has been the basis of several extensions which facilitate the numerical work, by С M Albone (1971) and by P R Garabedian & D G Korn (1971). It has also been successfully extended to deal with supercritical flows, as will be discussed in Section 4.8. Sells uses conformal mapping – which has to be done numerically – of the region exterior to the aerofoil in the physical plane onto the interior of the unit circle in the working plane. In this way, the unbounded region of the physical flow is transformed into a finite closed region suitable for numeri­cal work. How very well the results of Sells’s method agree with experimental results may be seen from an example given by R C Lock (1975) for the NACA 0012 aerofoil section with t/c = 0.12 at a = 0 and Mo = 0.74. Another comparison between Sells’s results and various approximations for a lifting elliptical aerofoil has shown that the simple Prandtl-Glauert rule is quite inadequate, and also that a consistent method by W Gretler (1965), which includes all second-order terms, is still not good enough. Evidently, higher-order terms play a significant part. On the other hand, empirical compressibility correc­tions derived by P G Wilby (1967) and by R C Lock et at. (1968) and also the Weber rule may give good answers. We shall have to fall back on such empirical factors when we discuss threedimensional wings in Section 4.4.

All these remarks apply only to a particular kind of compressible flow. Math­ematically, the term Vx/a in (2.6) must be smaller than unity, and the equa­tion is then of the elliptic type. As soon as Vx/a exceeds unity in a two­dimensional flow, the equation changes type and becomes hyperbolic. The main­stream Mach number at which this changeover occurs is called the critical Mach number. Slower flows are called subcritical and faster flows supercritical, and we speak of transonic or mixed flows when the flowfield contains several regions in which different types of equation apply. These distinctions go to­gether with fundamental physical changes. These and the definition of critical conditions will be discussed in more detail in Sections 4.2 and 6.3.

The physical changes can readily be seen in the simple case of the inviscid flow through a straight tube or pipe, which is onedimensional. The subcritical or subsonic flow is trivial: just a parallel flow with all flow parameters con­stant across and along the tube. But when the upstream velocity is greater than the velocity of sound – when it is supersonic – two states are possible: the flow may continue uniformly at the same speed, or it may go through a shock­wave and become subsonic downstream of it. In going through the shockwave, density and pressure are increased, but the velocity is reduced. Mathematically, a shockwave is a discontinuity but, physically, viscosity and heat conduction must have a dissipative effect and make the changes gradual. It turns out, however, that the extent of this region is of the order of the mean free path of the gas molecules and thus the concept of a discontinuous change is an admiss­ible approximation when the gas can be regarded as a continuum. The compres­sion through a shockwave is associated with energy losses*) and the entropy of

■’Strictly, no energy is ever lost. Whenever we loosely use this term, we mean that the available energy is reduced by transfer into other forms of energy, such as heat, which cannot be utilised by the system under consideration for the purpose we have in mind. See also Section 3.6.

the gas increases. Therefore, the reverse motion – an expansion or rarefac­tion shock – is not physically possible, because the entropy change through it would be a decrease. Thus expansions in supersonic flows are gradual.

Since we are interested in the aerodynamic design of aircraft, we note here that shockwaves and expansions in supersonic flows may be useful flow elements whenever we want to generate pressures over a body, which are either higher or lower than the mainstream pressure. Specifically, when we want to generate lift forces through a compression of the air underneath a body, then one or several shockwaves will serve that purpose. But we shall have to pay for it because of the energy losses involved, i. e. the energy available to do useful work is reduced. Lift generated in this way will be accompanied by a drag force, a wavedrag.

When the mainstream is supersonic, the concept of small perturbations may again be used in some cases to derive a powerful linearised theory for super­sonic flows – a counterpart to that described for subsonic flows in Section

2.2. Practical applications of this theory, which help us to order our thoughts, will be described in the appropriate places below. The method of singularities can also be extended to supersonic flows (see the textbooks listed above; also E Leiter (1975)).

2.4 Viscous interactions – flow separations. We have already mentioned the concept of the boundary layer which forms along solid surfaces and which allows the flowfield to be subdivided into an outer region, where the flow is regarded as inviscid, and an inner region, where it is essentially viscous.

The flow within the boundary layer may be laminar or turbulent or in a trans­itional state in between. The boundary layer grows as it flows along and we have already seen that this produces a displacement effect on the outer stream. Thus the pressure distribution over a body results from the combined effects of the inner and outer solutions, and the overall flow can only exist if both the inner and outer flows are physically possible and compatible so that their interactions are such that they can be matched. This concept of matched flows is of great practical importance, and we shall find that there are cases where the flow in the boundary layer, say, develops in such a way that the particu­lar type of flow reaches a state where it can no longer exist and where it must change. It may then happen that the whole flow pattern must change with it into another overall pattern. This aspect of viscous interactions must be given the closest attention in the design problem: we always design aircraft to have a certain type of flow, and it is of vital importance that we know when this flow ceases to exist, that is, what the conditions are which deter­mine the physical limits of its existence. In most cases, such a departure from the design flow has undesirable consequences, especially when the resul­ting new type of flow is unsteady. What one would really like is to design the aircraft in such a way that it returns by itself, without oscillations, to the design type of flow after an inadvertent excursion beyond its boundary.

But there are also cases where an aircraft may be required to fly safely beyond these limits.

Viscous interactions are the most frequent causes of such flow breakdowns, and that is one reason why a thorough knowledge of the development of the boundary layer is so important in practical applications. On a lifting wing, the boun­dary layer is, in general, subjected to an external flow with pressure changes which are large, especially at subsonic and transonic speeds, where most of the lift is generated by suction forces, that is, pressures below that of the main­stream. As we shall see in more detail later, this suction should be as high as possible and act over as large a part of the upper surface as possible.

This implies that, downstream of the suction region, the pressure must rise as steeply as possible so as to come back to some value near that of the main­stream at the trailing edge of the wing. The boundary layer can, therefore, be regarded as another design mechanism which produces or sustains compressions in the flow, or pressure recoveries. To be of practical use, it must be pos­sible to fit the boundary layer between an external compressive flow and a solid wall, and it must remain attached to the wall throughout this adverse pressure gradient. Again, we must pay for this because there are energy losses involved, in the form of a reduction in the momentum of the boundary layer and in the total head, and because the boundary layer forms a wake as it leaves the wing. Thus lift generated in this way will again be accompanied by a drag force, a viscous drag, part of which will be manifested as skin – friction forces along the surface and another part as pressure forces.

Apart from boundary-layer flows in adverse pressure gradients, we need to know many other properties, such as how and where transition from the laminar to the turbulent state occurs. Transition is one of the fundamental phenomena in fluid mechanics, which has received much attention from the earliest days but has so far defied our understanding in many of its aspects (see e. g.

L F Crabtree (1958), I Tani (1969), M V Morkovin (1969), M G Hall (1971),

E H Hirschel (1973), E Reshotko (1975). In aircraft design, all this needs to be worked out for threedimensional flows about rather complex shapes, not just for the twodimensional flow along a flat plate.

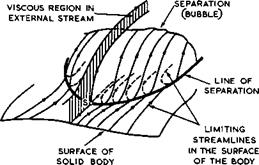
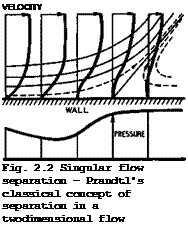
Perhaps the most important boundary-layer phenomenon is flow separation. Its treatment presents formidable difficulties, conceptually, experimentally, and theoretically. It is fairly easy to see why flow separation may occur in a boundary layer when it is subjected to an adverse pressure gradient, if boundary-layer concepts hold. Then the slower particles within the boundary layer have to flow against the same pressure rise as the faster particles in the outer stream. Both will be retarded but the particles within the boundary layer more so, because their kinetic energy is less, especially for those par­ticles nearer the wall where skin friction holds them back. The velocity pro­files through the boundary layer will then deform in the manner indicated in Fig. 2.2, which represents Prandtl’s classical model of flow separation: the flow lifts off the wall at a separation point where the skin friction becomes zero and the air flows backwards behind it.

This classical flow model has been the basis of numerous investigations, and many criteria have been put forward to predict the onset of separation and to describe the behaviour near the separation point. We mention here the crite­rion of В S Stratford (1959), which formulates the observation that turbulent boundary layers can withstand a larger pressure rise than laminar layers. How­ever, the usefulness of Prandtl’s flow model is limited if we want to know what happens on aircraft. The model refers to a hypothetical twodimensional steady flow and it does not tell us what the consequences of the flow separa­tion are (Prandtl recognised this and put forward some possible flow patterns which we shall discuss later). What we have already mentioned could very well happen, namely, that the interaction between the inner and outer flows is such that the overall flow patterns will break down and must change. In that case, the whole pressure field may also change significantly and the condition which led to separation at that particular point may no longer apply. The resulting flowfield may differ substantially from the one we started from, and separa­tion may be located at a different point.

Consider, for example, the simple case where the outer flow was initially strictly twodimensional and steady. If flow separation occurs, we have no reason to suppose that the resulting flow should also he twodimensional and steady. We have no means of telling why it should not acquire, say, some span – wise periodicity across the stream, or why it should not be time-dependent, with the separation point oscillating to and fro. Even if the flow with separa­tion did remain twodimensional and steady, the separation point need not be at the position calculated by boundary-layer theory for the pressure distribution of the initial flow without separation. It is vital to know about these matters in aircraft design and to be able to predict them and, if necessary, to avoid them. And all this must be clarified, of course, for the real three­dimensional flow. Here lie the real difficulties, and much remains to be done

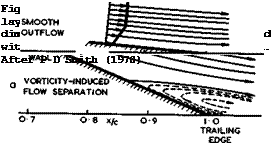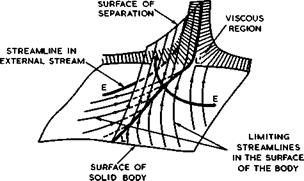
Before we proceed to discuss what little we know about these matters, we re­mind ourselves that the classical model of flow separation, based on the boun­dary-layer concept and viscous shear forces, is not the only mechanism that can lead to separation in twodimensional flows. Another possible mechanism is illustrated in Fig. 2.3. This type of flow occurs typically near the sharp

trailing edge of an aerofoil and is, therefore, of practical importance. The two boundary layers from the upper and lower surfaces meet and form a wake, and the confluence is characterised by curved streamlines, so that vorticity generated further upstream in the two viscous layers is transported along curved paths. This induces a velocity field (which is usually ignored in boun­dary-layer theory because one thinks primarily in terms of a flow along a flat wall where these induced velocities are zero, to a first order); it can readily be seen that these induced velocities will have a component which is directed against the flow and will retard it. If the vorticity is strong enough
and if the curvature is large enough, this retardation may bring the flow near the wall to a halt and make it separate. This flow model has been proposed by D Kllchemann (1967) and investigated by P D Smith (1970). J E Green (1972) has discussed some of the implications of this separation mechanism. Fig. 2.3 shows two such flows, one with smooth outflow and one with separation, caused in this case entirely by vorticity-induced velocities and not by viscous forces. In fact, the results have been calculated by P D Smith for an inviscid but rotational flow in a layer near the surface and in the wake.

This concept of an inviscid shear flow can be quite useful in some cases.

Flow separation in three dimensions is closely associated with the fact that streamlines near a solid surface are, in general, not parallel to the surface. The concept of crossflows is introduced to indicate that there are velocity components inside the boundary layer, which are normal to the velocity vector just outside the boundary layer, when the outer flow is threedimensional with curved streamlines. Further, the concept of limiting streamlines in the sur­face is introduced to indicate the direction of the streamlines as z 0 , when the streamlines become otherwise parallel to the surface. Limiting streamlines lie closely along skin-friction lines. But streamlines can also greatly increase, or decrease, their distance from the surface in the neigh­bourhood of certain lines. These are the ordinary separation lines (as opposed to the singular separation line in Fig. 2.2), where the flow lifts off the surface and where a surface of separation is formed. Ordinary separation lines are very important in practice, as are their opposite counterparts, the ordinary attachment lines, which may be regarded as a physical generalisation of what is usually called a stagnation point in twodimensional flows.

Threedimensional flow separations have been recognised as an important pheno­menon only fairly recently. We refer to fundamental papers by E C Maskell

(1955) , E A Eichelbrenner & A Oudart (1955), R Legendre (1956), and M J Lighthill (1963), where the main topological features of flow separation in three dimensions are described. More recently, J H В Smith (1975) and D J Peake & W J Rainbird (1976) have given extensive reviews of separation in steady threedimensional flows. We illustrate the main concepts by a few examples.

Fig.2.4 shows the typical herringbone pattern of the limiting streamlines in the surface near an ordinary attachment line (A). This could be the frontview

Frontvicw Sideview Fig. 2.4 Attachment flows

of the flow over a rounded swept leading edge, but patterns like this must occur in the flow past all threedimensional bodies of general shape. In the sideview, an attachment flow may look like the familiar twodimensional flow near a stagnation point, but this should be regarded as a singular case. Part of the curved flow is within the viscous region (between the dashed line and the body in Fig. 2.4), and the state of the boundary layer may already be determined here. A laminar boundary layer beneath such an external flow may be unstable to small disturbances and eventually become turbulent in the man­ner described by GHrtler (see e. g. P Colak-Antic (1971)). Alternatively, the flow along the attachment line may become turbulent by what is called contami­nation. In that case, there is also the possibility that the flow may revert to the laminar state because of the strong divergence in the flow, which may have a stabilising effect. These are important matters in aircraft design, but very little is as yet known about what happens in practical situations.

Fig. 2.5 Planviews of two types of flow near a swept leading edge

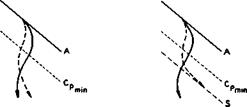
Next, we consider the flow further away from an attachment line where the streamlines in the outer flow are, in general, curved. Fig. 2.5 shows typical examples which may be interpreted as planviews of flows downstream of a swept leading edge. In these curved flows, the particles are subjected also to cen­trifugal forces, but the pressure may still be assumed to be roughly the same throughout the boundary layer. It then follows that slower particles nearer to the wall must follow a more highly-curved path (dashed lines in Fig. 2.5) than faster particles further out (full lines), to maintain equilibrium. This characteristic feature has important consequences. One is that these effects of curvature may lead to yet another mechanism to make laminar boundary lay­ers turbulent, in addition to that usually described as Tollmien-Schlichting instability. This is the Owen or sweep instability, which may imply that the laminar run in the threedimensional flow over swept wings may be shorter than that on a corresponding unswept wing where the flow is more twodimensional in character. Another consequence of the curvature may be the occurrence of a flow separation. According to E C Maskell & J Weber (1959), four different cases may be distinguished as far as the pressure field in such a flow is con­cerned, from one which makes flow separations impossible to another which is wholly favourable to the occurrence of flow separations. The latter is the one where the pressure rises rearwards as well as inwards, and this is the one that normally occurs behind the suction peak (marked Cp min in Fig. 2.5) on a sheared wing. Along the line of the suction peak, the curvature of the streamlines in the outer flow changes sign, and the streamlines curve outwards downstream of the peak. Streamlines within the boundary layer follow this pattern but, as explained above, the curvature must be higher. In the case shown on the lefthand side of Fig. 2.5, the curvatures are small enough for the flow through the whole boundary layer to continue regularly but, in the case on the righthand side, the limiting streamlines in the surface are suf­ficiently curved to point eventually in the same direction and to run tangen­tially into a single line and to have a cusp on that line, as Maskell des­cribed it. This then is an ordinary separation line, as defined above. It can clearly be observed experimentally in oilflow patterns on the surface. A streamsurface of separation originates from that line. What matters is that the air near the surface of the body does not flow past the separation line and that we must find out, in any given case, the shape of the separation surface and the nature of the flow beyond it.

We can make a fundamental distinction between flows where the part of the body surface beyond the separation streamsurface is wetted by mainstream air and flows where it is not. These two typical cases of separation from a general curved surface are illustrated in Figs. 2.6 and 2.7, where the possible extent of the viscous region is also indicated; the flow external to this region may be considered as predominantly inviscid. Fig. 2.6 represents the case where a bubble is formed, whereas Fig. 2.7 represents the formation of a

SURFACE OF Fig. 2.6 Separation in a threedimensional flow, leading to a bubble with a singular separation point S

Fig. 2.7 Ordinary separation in a threedimensional flow, leading to a vortex sheet

free shear layer acvortex sheet. In the first case, the surface of separation encloses fluid which is not part of the mainstream but is carried along with the body; in the second case, the space outside the body on either side of the surface of separation is filled wholly by mainstream fluid. The limiting streamlines in the surface are indicated and also how they join the separation line, in a reversed herringbone pattern, and then form the surface of separa­tion. The bubble formation requires the existence of one singular point S (a saddle point), where the behaviour of the flow is similar to that near a separation point in twodimensional flow. All other points along the lines of separation in Figs. 2.6 and 2.7 are ordinary separation points, as defined by Maskell. These examples explain why concepts based on twodimensional flows, where separation lines must be normal to the mainstream and composed of singular points, are of little use in the discussion of flow separation in three dimensions.

The examples in Figs. 2.6 and 2.7 also serve to show that, while the concepts of boundary-layer theory may be applicable upstream of and away from the sepa­ration line on the body, they are clearly not adequate in the neighbourhood of the separation line. The viscous region around the surface of separation does not necessarily possess the properties of a boundary layer either. The shear layer in Fig. 2.7 may be thought of as a surface of discontinuity, or thin vortex sheet, in its effects on the mainstream, if the Reynolds number is high enough. In the case of Fig. 2.6, slow viscous eddies will rotate inside the closed bubble and form an essential part of the flow. In practice, a combination of the two types of flow with a bubble and with a free shear layer may also occur. Maskell showed how each type of flow is characterised by a particular form of surface flow pattern and demonstrated how this approach can greatly simplify the construction of threedimensional skeletons of complex flow patterns. It is essential to clarify these in any given cases all too often, threedimensional flow patterns are misinterpreted.

Some examples of practical importance are sketched in Fig. 2.8 in a simplified form as the traces of the separation surfaces in a plane normal to a leading

a Low sweep b Moderate sweep C High sweep Fig. 2.8 Various possible shapes of threedimensional separation surfaces

edge near which separation is assumed to occur along a line marked Sj. The angle of sweep of the edge is varied. At zero or small angles of sweep, Fig. 2.8a, the flow may be nearly twodimensional and a closed bubble may be formed, i. e. the surface of separation reattaches to the body surface and contains a slowly rotating flow which is not part of the mainstream air. Such a flow is not strictly steady, but the concept of time-average streamlines is still useful. At the other extreme of high angles of sweep, Fig. 2.8 c, the flow is essentially threedimensional; the separation streamsurfaces are all open and the whole space is filled by mainstream air. This type of flow is usually quite steady. The separation surfaces may be interpreted as vortex sheets which roll up along their free edges into coiled vortex cores. These cores grow in space, as further vorticity is fed into them. There is usually another attachment surface, intersecting the body at Aj, which divides the air that is drawn into the vortex core from that which passes it by. In general, a secondary separation line S2 and a secondary vortex sheet are formed, because the air near the surface of the body is not able to run up against the adverse pressure gradient which must exist once the air has passed underneath the main vortex core, which induces a suction peak on the surface.

In principle, the process whereby further separation lines and vortex sheets are introduced may be continued indefinitely but, in real flows at finite Reynolds numbers, this process is terminated when the boundary layers and vortex sheets are no longer thin and when the little sheets are swallowed up by the viscous fluid surrounding them. Between the two extreme cases, there may be an intermediate type of flow at moderate angles of sweep, Fig. 2.8 b, which involves a bubble with at least two eddies of opposite sense inside it as well as a free surface of separation with a rolled-up core.

Closed bubbles with reattachment and coiled vortex sheets are concepts which play a very important part in aircraft design, and we must now look at some of these flew elements in more detail. Consider first flow elements which in­volve mainly bubble separations, as they have been described by L F Crabtree

(1957) and I Tani (1964). The front part of the surface of a bubble can usually be regarded as a thin curved shear layer, along which the pressure is nearly constant and below that of the mainstream. There is little flow inside this part of the bubble. To bend the shear layer back towards the surface of the body and to make it reattach requires a pressure rise, and this must be matched by a pressure rise in the outer flow. In the bubble, the pressure rise must be supplied by a viscous process: we say that the air in and near

the shear layer undergoes a process usually described as turbulent mixing.

This can indeed produce a rise in pressure along time-average streamlines and also in the outer flow where the streamlines lose some curvature as a result of a considerable thickening of the viscous region. For this to occur, the shear layer itself must first be turbulent. This leads to an essential dis­tinction between two different types of flow in those cases where the shear layer is the result of the separation of a laminar boundary layer and where it is laminar itself to begin with. Transition to the turbulent state must then occur in the shear layer on top of the bubble before the layer can re­attach to the surface through the mechanism of turbulent mixing. How and where this happens affects the size of the bubble: depending on whether transition occurs after a short run or a long run, the bubble is either short or long, compared with the dimensions of the body. P R Owen & L Klanfer (1953) have derived a criterion to distinguish between the two ‘types of bubble. In general aircraft applications, the short bubble is a useful flow element, the long bubble is not.

The turbulent reattachment usually takes a relatively short length of the order of ten bubble heights or less downstream of transition. We can visualise

Fig. 2.9 Flows with turbulent reattachment

this part of the flow in terms of the sketch, Fig. 2.9 a. This is closely related to the flow with a pressure rise in a pipe or duct with a sudden enlargement of the cross-section, as sketched in Fig.2.9 b. There is again a bubble separation with reattachment, and the stream is assumed to be uniform far upstream (suffix 1) and again far downstream (suffix 2) if complete mix­ing has taken place. In this case, a pressure-rise coefficient can be deter­mined by application of the momentum theorem. Expressed in a canonical form in terms of the initial dynamic head JpV-^2г this gives

(2.39)

where V are velocities and A cross-sectional areas. It is assumed here that the pressure over the rearward-facing base is constant and equal to p^. This very simple flow model, which can easily be realised in practice, tells
us that the pressure rise which can be obtained by a mixing process is limited. The value of a according to (2.39) has a maximum which is 1/2.

The flow at the rear end of a closed bubble differs from pipe flow in that there is only one wall so that some air may flow into (or out of) a cylindri­cal surface of integration (dashed line in Fig. 2.9 a). Momentum can then be added during the mixing process and transferred into an additional pressure rise, so that the pressure-rise coefficient, though still limited, has a max­imum value which can be greater than 1/2. This momentum transfer through entrainment could thus allow a greater pressure rise to be sustained, but the actual amount will depend on how this mixing flow can be matched to the exter­nal stream. The existence of a maximum pressure recovery seems to imply that there is also a maximum possible shear stress in the turbulent entrainment. A somewhat different, but basically similar, pressure recovery coefficient has been used by A Roshko & J C Lau (1965) in their investigation of the reattach­ment of free shear layers.

This type of flow, which relies so much on vigorous turbulent mixing, is ne­cessarily associated with energy losses which are likely to be greater than those associated with turbulent boundary layers. Even so, it is used in air­craft design (mainly in the form of short bubbles) simply because it offers another viscous flow element which can be matched to an external flow with pressure rise, under certain conditions. There are so few of these! But the existence of a maximum pressure rise implies that a matched flow may break доит altogether when subjected to even relatively small changes. Long bubbles on aerofoils can adjust themselves fairly readily by getting longer until their tailend sticks into a region in the external flow where the required pressure rise is smaller and does not exceed the limiting value. If need be, long bubbles extend beyond the trailing edge into the wake. Short bubbles cannot do this: they burst. The maximum value of the pressure-rise coeffi­cient a has been found to be about 0.35 in incompressible flows about aerofoils; when the external flow demands more than this, the bubble bursts and the whole flow pattern breaks down and changes radically. It then includes a large-scale flow separation, whereas before it may have given the appearance of an attached flow, because short bubbles are normally so very small, compared with the dimensions of the aerofoil (see also Section 4.7,

Fig. 4.40). Another criterion for bubble bursting has been given more recently by F X Wortmann (1974).

At low speeds, the external compressions are necessarily gradual, but discon­tinuous compressions in the form of shockwaves may occur in transonic and in supersonic streams. In aircraft design, especially for transonic speeds, one likes the shockwaves to be rather strong, as we shall see in Section 4.8. We are then faced with the problem of finding a viscous flow element which can be fitted between the foot of the shockwave and the solid wall. A short bub­ble can serve this purpose, and so the combination of a shockwave and a turb-

Fig. 2.11 Shock-induced bubble separation

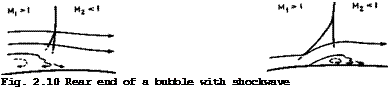
ulent mixing region is of practical interest. A simple combination of these flow elements is sketched in Fig. 2.10, which can be interpreted as the re­attaching flow at the end of a bubble underneath an external flow which goes from a supersonic speed to a subsonic speed through a shockwave. To a first approximation within the concept of boundary layers, the pressure rise through the unswept normal shockwave and that through the mixing region must be the same and hence

Thus the upstream Mach number Mj is limited by the pressure rise that can be provided by the mixing process, so that

for air. We have = 1.2 for a = 1/2, but Mj could be greater than 1.2 if momentum transfer by entrainment could increase the value of a . This would be very welcome in aircraft design but we do not yet know how to bring this about.

The sketch in Fig. 2.11 illustrates a more complete flow pattern, showing the whole bubble separation with reattachment underneath a normal shockwave which may be thought of as terminating a local supersonic region over an aerofoil. This simplified flow model is based on observations made by J Seddon (1960) .

It incorporates a distinctive forward leg at the foot of the shockwave so that in some region above the bubble, there are two compression processes in series one through this forward oblique shock, matched by a pressure rise in the separating boundary layer underneath, and another through the rearward leg of the shock, matched by the pressure rise from turbulent mixing during the re­attachment process. In Seddon’s experiment, = 1.5 could be realised.

The forward leg reduced the local Mach number to about 1.2 and the rearward leg together with turbulent mixing reduced the Mach number further from 1.2 to a subsonic value. So we arrive at a flow model which is at least reason­ably consistent. But the difficulties which are involved in developing this into a method suitable for practical design purposes have not yet been over­come. These are formidable, both theoretically and experimentally, because both the outer inviscid flow and the inner viscous flow are very complex.

Consider now flow elements which involve mainly vortex-sheet separations (see e. g. D Klichemann & J Weber (1965), J H В Smith (1975)). We note first that the concepts discussed so far result mainly from thinking about essentially

twodimensional flows. However, it is doubtful how far they apply to the three­dimensional flows, like those over swept wings, which are of real practical interest. There is no doubt that Fig. 2.11 does not apply when the shock is highly swept in planview. In that case, we may still expect that a flow separation occurs at the foot of the shockwave, but the separation surface can then take the form of a vortex sheet, as sketched in Fig. 2.12. The flow direction immediately behind the foot of the shockwave is then reversed and the air actually experiences a fall in pressure which is, nevertheless, compatible with a pressure rise through the shockwave in the external stream. These glancing interactions have been the object of some study (see e. g. A Stanbrook (1961)), but we know very little about their occurrence on swept wings where, again, they constitute a departure from twodimensional flow concepts.

Shockwaves and vortex sheets need not only occur in the combination shown in Fig. 2.12 but also in the form sketched in Fig. 2.13. Here, the vortex sheet may have been generated further upstream, perhaps under conditions where the flow was still subcritical, as in Fig. 2.8 c. At supercritical conditions, the flow may expand over the outside of the vortex sheet and a local super­sonic region may be formed there, terminated by a shockwave. Compared with the more familiar local supersonic region over the front of a twodimensional aerofoil section, the whole region is now lifted off the surface. Such flows can exist only in three dimensions and are, therefore, of particular interest for swept wings. A vortex core is then formed and must expand in the spanwise direction, if the flow is to be steady. A conical flow of this kind has been observed by D Pierce & D A Treadgold (1964), and there are indications that similar flows may exist on threedimensional swept wings. This applies when the angle of sweep of the separation line is high, but very little is known about what happens at moderate angles of sweep and about how wings could profitably be designed to have this type of flow. All these are typical examples which demonstrate clearly that we are concerned with matters where any progress made in research on fundamental flow mechanisms could be exploited immediately and profitably in practical applications.

In most of the flow elements considered so far, separation was assumed to occur somewhere along a smooth surface. There is no reason and no evidence to suppose that the resulting separated flow should always be steady. But flow steadiness is one of the essential requirements in aircraft design, and that is why we are vitally interested in fixing separation lines at some well – defined place and in keeping the separation lines firmly under control. So far, the only concept we can think about as one which will fix flow separation is the aerodynamicatly sharp edge. This may be defined as a geometric shape where the curvature is very high, or even infinite, so that the inviscid flow would acquire a very high, or even infinite, velocity and consequently a very high, or even infinite, adverse pressure gradient. This is meant to make the separation of a real viscous flow around this shape inevitable. We then say that the Kutta condition is fulfilled at such an edge and we mean by that that the outflow is smooth and that any infinite velocity or pressure gradient has been removed. This definition can also lead us to a useful approach to deal with the problem of fulfilling the Kutta condition. First, we think of the flow with a singularity at the edge, which an inviscid flow could make; second, we devise another flow which, when combined with the first, will remove the singularity. This approach has been used successfully by E C Maskell (1960) (see also D L I Kirkpatrick (1967)) in dealing with the flow separation from the leading edges of a slender wing, which will be discussed further in Sections 6.3 and 6.4.

We have already seen an example of a smooth outflow from an unswept sharp trailing edge in Fig.2.3(b), with separation confined to. the trailing edge only. In this simple case of a symmetrical body, an inviscid fluid can already flow smoothly from the trailing edge, and there is no particular difficulty in fitting a rotational or viscous flow into it, provided the flow reaches the trailing edge and does not already separate upstream of it. Matters are more complicated when the flow is not symmetrical on either side of the edge, as on an aerofoil put at an angle of incidence, and when two flows of different directions and/or speeds meet at some edge. As Helmholtz has said in 1868,

"any geometrically sharp edge must tear apart the fluid which flows past it and produce a surface of discontinuity, even when the remaining fluid moves only at moderate speeds".

How this tearing-apart may happen and how the Kutta condition of smooth out­flow may be fulfilled is a very important matter, which has been discussed and clarified more recently by К W Mangier & J H В Smith (1970), R Legendre

(1972) , and E C Maskell (1972). We want to illustrate this flow by three examples in which inviscid flows with edge singularities are converted into flows with smooth outflow, and the singularities removed, in three entirely different ways. We may think about them by visualising first inviscid flows with infinite velocities at the edges of thin solid plates and then converting these into real flows by the sudden application of viscosity. (Alternatively, the real flows can be thought of as being brought about by a starting process during which the air or the body are suddenly set in motion). In all three cases, the resulting flows can again be regarded as inviscid – the part that viscosity plays is to establish them.

Fig. 2.14 shows on the lefthand side the initial flows to be considered:

(a) the steady twodimensional flow past a flat plate at a small angle of in­cidence to the mainstream; (b) the steady twodimensional flow past a flat plate at right angles to the mainstream or, alternatively, the steady flow in a crossflow plane through a threedimensional slender wing; and (c) the steady twodimensional flow along a flat plate which separates two streams of differ­ent velocities and different total heads. In all three cases, the air far downstream settles down to a uniform parallel flow as though nothing had hap­pened. The converted flows are shown on the righthand side of Fig. 2.14.

They are quite different. The possibility that bubble separations occur has been excluded and, in all three cases, the sudden application of viscosity is supposed to lead to the formation of a surface of discontinuity, or vortex sheet, which rolls up into at least one coiled vortex core along the free edge. As we shall see later, such a vortex core is a powerful mechanism for concen­trating energy, which in turn induces a strong velocity field. This may be regarded as the physical means whereby the flow near the edge is straightened out.

In case (a), a starting vortex is formed, which is then carried downstream with the flow while the strength of the connecting vortex sheet gets weaker and weaker and becomes zero when the starting vortex reaches infinity. Thus the resulting flow is steady again and very simple. It seems almost literally "straightforward" to fit a viscous region in the form of a thin boundary layer and a thin wake into it. (However, closer inspection reveals many complexities see e. g. S N Brown & К Stewartson (1970)). Apart from small-scale turbulent fluctuations in the boundary layer and wake, the flow can be expected to be steady on time-average.

In case (b), at least one pair of strong coiled vortex cores is needed to straighten out the flow at the two edges. If the flow is meant to be two-

dimensional, it must become time-dependent, as the vortex cores grow as a con­sequence of a certain mass of air being fed into them; they will also be left behind in the flow. If the flow is meant to represent the crossflow over a threedimensional slender wing, then the two cores will grow in space over the wing to accommodate the air. The flow is then similar to that sketched in Fig. 2.8 c. Again, viscous regions can readily be fitted into this flow pattern in the form of thin boundary layers and thin shear layers, if the Reynolds number is high enough, without upsetting the general characteristics. The threedimensional flow can be expected to be steady.

In case (c), the resulting flow is again time-dependent, vortex cores being swept downstream. In the general case with different speeds and different total heads in the two streams, a steady smooth outflow as in case (a) cannot exist unless the two flows are perfectly matched, which, in real flows, must include conditions for the densities and temperatures. In one possible mechanism, we may expect that a core with concentrated vorticity could do the job initially (as in the second case), but that another core is needed as the first is floating downstream and then yet another and so on. Thus, in this case, a possibly periodic succession of vortex cores may be needed to keep the flow straight near the edge and to maintain the velocity difference further downstream. Since this type of flow may be interpreted as representing part
of a nozzle from which a jet emerges, and since the velocity difference is then essential in practice so that kinetic energy is left behind in the jet, the Kutta condition appears to imply that, in this particular type of flow, the flow in the boundary of the jet is essentially unsteady and involves an array of vortex cores. The disturbances caused in this way must be expected to generate noise in the outer flowfield (see S M Damns & D Ktlchemann (1972)).

We note that the three mechanisms which are used to satisfy the Kutta condi­tion differ remarkably from one another. The first case is easy and almost trivial; the second case can lead to a steady threedimensional flow, but powerful concentrations of vorticity are needed to ensure smooth outflow; and the third case can lead to a time-dependent flow with periodic genera­tion of concentrated vorticity.

In the last two cases, the formation of a surface of discontinuity in the form of a coherent vortex sheet as a result of flow separation is an essen­tial mechanism, and we shall see later that flows like that in the first case do occur on threedimensional wings where again a vortex is generated at the separation line along the trailing edge. Thus vortex sheets are an important concept in aircraft aerodynamics, and there are many cases where the model of a thin vortex sheet in an otherwise irrotational inviscid flow is admissible and useful. We may consider such flows as being composed of three distinct elements: A solid body, one or several vortex cores, and outer connecting

vortex sheets linking the two others. Continuous vortex sheets are at all times formed by the same fluid particles which carry their vorticity with them. Further, the static pressure must be the same on either side of the sheet because it cannot take any force. These properties lead to boundary conditions for calculations but, so far, only a few particular solutions are known (see e. g. A Betz (1932) and (1950), M Stern (1956), D Ktlchemann & J Weber

(1965) , J H В Smith (1966) , D W Moore & P G Saffman (1973), D W Moore (1974) and (1975)). These vortex motions will be discussed further in Section 6.3.

The main theorems concerning vortex motions were established by H von Helmholtz (1858) and (1868) and by Lord Kelvin (1869) . They can be found in any good textbook on fluid mechanics. In aircraft aerodynamics, we are concerned not only with free vortex sheets but also with bound vortex lines by which we represent solid surfaces. These are hypothetical to the extent that they are regarded as capable of sustaining a pressure, and as not moving with the fluid.

The velocity field of an element of vortex line is given by Biot-Savart’s equation. To represent a flow by the sum of the induced velocities of a number of such singularities automatically ensures that the equations of inviscid flow are satisfied. Thus distributions of sources and vortices can be used to represent a thick lifting wing with a vortex wake.

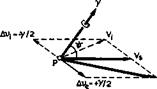
In Fig. 2.15 are sketched the conditions at a point P of a threedimensional vortex sheet, the tangent plane at P coinciding with the plane of the paper. V£ and Ve are the velocities on either side of the sheet. Vs = J (V£ + Ve) is the so-called mean velocity, and у is the vorticity vector which is per­pendicular to the velocities it induces on either side of the sheet. The general result for any vortex sheet is that the induced velocity increments are Ave = +y/2 and Avf = – y/2 and that у, Vi, and Ve are coplanar. у

has the dimension of a speed and represents the vortex strength per unit length of a vortex line.

If the suffixes і and e refer to the two sides of the sheet, Bernoulli’s

Fig. 2.15 Conditions at a point in the tangent plane of a vortex sheet

equation for steady flows may be written Hi = Pi + Jpv.2 ; H = p e ^e + Jpve2 . (2.42) Thus the pressure difference, Ap, across the sheet is Др = Pe – p. = AH + Jp(V.2 /—N CM 0) >  1 9 (2.43) AH = He – being the difference in total pressure. Elementary trigono­metry, applied to Fig. 2.15, puts (2.43) in the form

Ap = AH – pVgY віпф. (2.44)

This equation has obvious importance in dynamical problems and some particu­lar cases are now taken.

1 For a vortex sheet separating regions of equal total pressure, for exam­ple, a trailing vortex sheet, both Ap and AH are zero, and so ф is zero also. The velocities on either side of the sheet are then equal in magnitude and equally inclined to the vorticity or mean velocity vectors which are in the same direction.

2 If AH is not zero, as for the surface of a bubble, then ф is also not zero if the vortex sheet is such that Ap is necessarily zero.

3 In the case of a bound vortex sheet, such as that which represents a so­lid boundary, Ap is not zero. If the total pressure is the same on both sides, as is usual with a thin wing,

Ap = pVssini|/ , (2.45)

and the solid boundary must sustain this pressure difference. As an example, consider a thin unswept wing of large span. Except near the ends, the vorti­city vector is almost at right angles to the mainstream; thus ф – тг/2. Further, V8 may be taken as Vo, the speed of the stream at infinity. Therefore,

Лр = PV0Y » (2.46)

which is commonly called the Kutta-Joukowski theorem for the lift force. It holds for the local force from the vortex element; it is equally true for a whole wing. We shall return to these matters later when we discuss wing flows in more detail.

With regard to flows about the cores of vortex sheets, it is useful to distin­guish between threedimensional cores, which grot) in space, and twodimensional cores, which grow in time, and also between single-branched cores along the edges of vortex sheets and double-branched cores which the outer vortex sheets enter on one side and leave on the other. The key feature of cores growing in space is the strong interaction between swirl and axial velocity components in that the swirling fluid drawn into the core escapes in an axial direction and may acquire a high velocity along the axis, several times that of the main­stream. Twodimensional cores, where such an escape is precluded, must grow sufficiently in time to accommodate all the fluid: there is no twodimensional steady vortex-sheet core. In this respect, the traditional concept of a "line vortex", with a steady twodimensional flow like a potential vortex out­side and a solid-body rotation inside, is quite wrong. There are no physical means for producing it in an airstream. The fact that we can construct math­ematically exact solutions of the Navier-Stokes equations does not necessarily imply that they are physically realistic. We note in passing that, apart from the unrealistic line vortex, there are some other solutions which we actually have but cannot find a practical application for, at least not on aircraft aerodynamics. These are the group of exact solutions of the time – dependent Navier-Stokes equations for twodimensional swirling flows by C W Oseen (1912), J F Burgers (1948), and N Rott (1958).

How regions with concentrated vorticity can be generated in a fluid of low viscosity has been suggested by A Betz (1950). In view of the large kinetic energy in these swirling flows, he concluded they can only come about by the rotting-up of vortex sheets which originate from separation lines along solid bodies in the way described above. This is certainly confirmed in all known cases in aircraft aerodynamics, aand this is why the tightly-rolled vortex cores are so important in practice.

Fig. 2.16 Vortex sheets from long flat plates at an angle of incidence

Single-branched cores are formed as a rule on either side of the vortex-sheet wakes behind lifting wings. Double branched cores are less common. As far as we can see now, there may be several mechanisms to bring them about. One of these has already been described in Fig. 2.14 c. Another is associated with the big-scale flow about a lifting body when attachment and separation lines intersect on the surface of the body from which the vortex sheets spring, as illustrated in the lower part of Fig. 2.16 from observations by R L Maltby. It may be caused by putting a long flat plate of small aspect ratio with sharp

Fig. 2.17 Sketch of the shape of the vortex sheet behind a body moving uni­formly downwards in still air. After Pierce (1961)

side edges at a slight angle of yaw. Without yaw, the flow and the vortex system may be symmetrical, as in the upper part of Fig.2.16, with the attach­ment line running down the middle of the plate. With yaw, attachment is along a zigzag line which intersects first one edge, then the other, and so on, and this leads to the formation of a new core at every intersection. We note that the flow is not necessarily symmetrical even without yaw: the symmetry of a

body placed symmetrically in a stream does not ensure the symmetry of the vortex pattern; a periodicity in the vortex wake is always a possible alter­native.

Another mechanism is not necessarily associated with a big-scale flow but may be a property of the sheet itself together with possible fluctuations in the flow in the immediate neighbourhood of the separation line, even when the line itself is firmly fixed. A flow of this kind is illustrated in Fig. 2.17 from observations by D Pierce (1961). Evidently, a small-scale array of double – branched cores can be superposed upon a big-scale flow which itself can have a large core. We can even envisage a flow which incorporates both a periodic array of large double-branched cores and another periodic array of small and again double-branched cores along the sheet. All these can grow either in space or in time or in both. What is observed fairly often is uniform shed­ding of vorticity. This appears to lead either to cores growing approxi­mately conically in space or to cores growing approximately linearly in time.

2.5 Flows suitable for aircraft applications. We have recognised by now a number of basic types of flow and flow elements and can proceed to consider what properties they should have to make them suitable for engineering applications in aircraft design. As already explained in Section 1.4, such a selection of healthy engineering flows will then lead to certain classes of shape and, out of these, types of aircraft can be constructed. This line of approach – from flows to shape – is the key feature and probably the most important aspect of the design method adopted here. It is considered to be the main principle underlying rational aeronautical engineering. But this principle has also been questioned from time to time, and we must be aware of the temptation that lies in the apparent possibility of obtaining solutions out of the powerful tools that we now have, regardless of what the flows are like. It is also said some times that, given the large engine powers now available, one could make a barndoor fly. This is even true, up to a point, but it is not aeronautical engineering as we understand it here.

There are certain basic criteria which should be fulfilled for a flow to be considered suitable for engineering applications. In the first place, the flow should be steady and stable. This means that flows which fluctuate and oscillate with time are, in general, not suitable. Also, the flow should be well-defined and insensitive to disturbances which it will meet in flight through the atmosphere. Any perturbations should not upset the flow alto­gether. Instead, it should be stable enough to revert to its initial state. Next, the flow should be controllable. It should be possible to produce quite a range of forces and moments on a flying body over a range of flight conditions within which a certain type of flow can exist. Any changes in forces and moments should not be abrupt but gradual and smooth and uniquely deter­mined. The pilot should be able to perform readily all the manoeuvres which are required from the aircraft to fulfil its functions. Ideally, the type of flow should be the same throughout the whole flight envelope of the aircraft, but we shall allow certain exceptions to this rule, provided the changes from one type of flow to another are also gradual and smooth. Lastly, the flow should be efficient. This means that the generation of lifting and propulsive forces should not be accompanied by large energy wastage. The flows must all be such that work is done on the air by the flying body. The energy needed for this is carried along in the aircraft in the form of fuel, and what is wanted is that the available lift work is as large a portion of the heat con­tent of the fuel as possible. We shall discuss these matters in more detail in Chapter 3.

There are some general features which flows past aircraft must have, indepen­dent of what the particular type of aircraft is. Geometrically, the shape of any aircraft will have a certain streamwise extent, or chord, and a certain lateral extent, or span. This body will have a certain mass and volume and hence a thickness, which can be expected to be smaller than the chord and the span. Thus we consider rather flattish shapes. This body moves through the air, or the air moves past it, and, to counteract the gravitational force on its mass, the airflow must exert an equal and opposite force on the body to maintain level flight. This lift force appears primarily in the form of pres­sure forces distributed over the surface of the body. Clearly, a lift force is generated if the pressure over the lower surface is higher than the ambient pressure, or if the pressure over the upper surface is lower than the ambient pressure, or if there is a combination of both. This implies that we are always concerned with flows which divide along some attachment line along the front of the body and then experience different changes of condition, depend­ing on whether the particles flow below or above the body. Downstream of the attachment line, the two flows should remain attached to the surface of the body until they meet again at a separation line along the side or the rear of the body. This separation line should remain fixed in the same position under all flight conditions. In the general case, the flow conditions on either side of the separation line will be different. For example, the magnitudes and directions of the velocities may differ. This means that a surface of discon­tinuity, or vortex sheet, will be formed, as discussed above. Flows with thin trailing vortex sheets are eminently suitable for engineering applications and an essential feature of aircraft aerodynamics. Further, viscous regions should be thin, and so E C Maskell (1961) formulated the generalised design objective as the achievement of thin-wake flows.

These conditions mean that singular separations as in Fig. 2.2 are undesirable, especially when the resulting bubble is of the kind shown in Fig. 2.3(a) and occupies an appreciable region over the rear of the body. Also generally un­desirable are bubble and vortex-sheet separations if they occur on smooth sur­faces as in Figs. 2.6 and 2.7, so that the separation lines are not necessa­rily fixed. What is wanted are vortex-sheet separations from aerodynamically sharp edges, where the Kutta condition is fulfilled, as has been discussed in connection with the flows sketched in Fig. 2.14. We note in this context that this type of flow imposes a condition on the static pressure to be reached at the edge: it must be the same at either side of the sheet and also along the separation line; its value is usually not very different from that of the ambient pressure in the mainstream.

Other essential flow elements on lifting bodies are expansions and compressions. Under supersonic conditions, these may take the form of Prandtl-Meyer expan­sions around edges and of shockwaves. Compressive flows, in particular, must follow any expansions so that the pressure rises again from a value below that in the mainstream to the right value required along the separation line. It is one of the main problems in aircraft design to find shapes with pressure distributions in inviscid flows with just the right pressure gradients, into which viscous regions along the surface can be fitted without upsetting the overall flow pattern and without involving unacceptably large energy losses.

This is why turbulent boundary layers, which can sustain large compressions, and turbulent mixing regions, as in Figs. 2.9 and 2.11, are of such practical interest. To exploit the pressure rise associated with the reattachment pro­cess, it is even admissible to have a secondary separation with reattachment between the primary attachment and separation lines, provided the resulting bubble is short and small in extent compared with the dimensions of the body. Secondary vortex-sheet separations, as in Fig. 2.8(c), are also acceptable flow elements.

In the thin viscous regions, the displacement thickness should be thin so that the actual pressures over the body do not deviate too much from those in in­viscid flow and the pressure drag remains small. The momentum thickness of the boundary layer and of the wake should be thin so that the skin-frietion drag remains small.

Some requirements which concern the state of the boundary layer may be in con­flict with one another. With regard to overcoming pressure rises, we would like the boundary layer to be turbulent. With regard to keeping the skin-fric­tion drag low, we would like the boundary layer to be laminar. Under normal flight conditions, a laminar boundary layer would be thinner than a turbulent boundary layer and produce less skin-friction drag. It would also have a smaller heat transfer from the air to the surface of the body. This matters especially at supersonic and higher flight speeds, where such an energy trans­fer must be regarded as an unwanted loss, which introduces severe engineering problems in the construction of high-speed aircraft. Unfortunately, there are so many disturbances of various kinds in the flow past most aircraft that long runs of laminar boundary layers over an appreciable part of the surface of the aircraft are difficult to maintain. So far, only small aircraft, such as some gliders, have successfully been designed to exploit the properties of natur­ally laminar boundary layers. There is just a possibility that future high­speed aircraft, flying at high Mach numbers and altitudes, might again benefit from naturally laminar flows. The expected advantages are so great, especi­ally with a view to saving fuel in long-range transport aircraft, that they provided enough incentive to spend a great effort on solving problems of bound­ary-layer control, i. e. on finding artificial means for keeping the boundary layer laminar, for instance by sucking part of the boundary layer away into the surface (see e. g. 6 V Lachmann (1961)). Although some of these flow mechanisms have been put on a sound physical basis, they have not yet found lasting engineering applications.

There are many flow elements involving energy addition to an airstream which find practical applications in the generation of propulsive forces. One of these is that sketched in Fig. 2.14(c). We leave the discussion of others until we come to the actual applications in Chapters 3 and 8.

In all the subsequent and more detailed discussions, the emphasis will be put firmly on the physical characteristics of the flows we want to use in designs. This may seem antiquated and old-fashioned at a time when computational aero­dynamics is coming to the fore, and when there is a growing belief that, given big enough computers, all our problems can be solved numerically. The approach adopted here does not follow this trend: many approximate methods will be described simply because they bring out clearly the essentials of the behavi­our of the flows in crucial and critical regions, and because they give a sound basis for design. Computers, like windtunnels, are welcome and much- needed tools, but they do not make physical insight redundant.