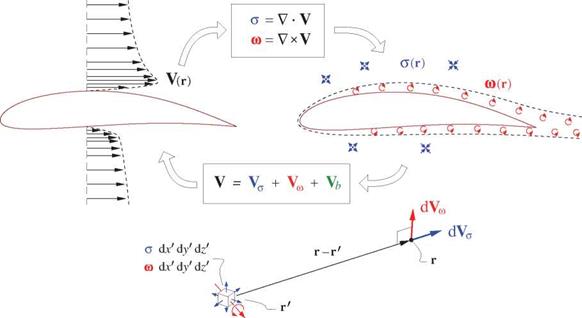
Velocity / Vorticity-Source Duality

The sheet strengths A and 7 in Figure 2.1 will be shown to be closely related to the source density a and vorticity ш distributions, which can be obtained from the velocity field by taking its divergence and curl.

a(r) = V-V (2.1)

ш( r) = VxV (2.2)

Conversely, the velocity field can be obtained from the source and vorticity fields via definite volume inte­grals over the entire flow-field. This in effect reverses the divergence and curl operations, as discussed by Batchelor [2] in some detail. These reciprocal operations are illustrated in Figure 2.2, and given as follows.

V(r)	= Vo + V + Vb	(2.3)
where Vo (r)	– iJIIa{”’ r-rf dX’iV’d‘	(2.4)
Vw(r)	= 4ТГ j®^(r,)X|r-r’|3 dx>dy>dz>	(2.5)
Vb	= Vo (for unbounded external flow)	(2.6)

Figure 2.2: A flow velocity field V(r) shown on the left can be used to define the source and vorticity fields a(r) and ш(г) shown on the right, and vice versa. Boxes contain reciprocal conversion relations from one description to the other, with Vo – and Vu defined by equations (2.4) and (2.5).

The infinitesimal volume element dx’dy’dz’ at the integration point location r’ with source density a(r’) and vorticity w(r’) has contributions to the total V(r) at the field point at r. The source contribution dVo – is parallel to the connecting vector (r — r’), whose explicit definition and magnitude are as follows.

r — r’ = (x—x’) x + (y—y’) y + (z — z’) z (2.7)

|r-r’| = J{x-x’]2 + (y-yO2 + (z-z1)2 (2.8)

The vorticity contribution dVw is perpendicular to both (r — r’) and ш.

The last velocity component V/, in (2.3) is the part of V which has both zero divergence and zero curl everywhere in the flow-field, and hence cannot be represented by a or ш within the flow-field. In the typical external aerodynamic flow extending to infinity, V is a constant field, and equal to the freestream velocity as given by (2.6). In the more general case, such as flow near a wall or inside a wind tunnel, Vb is not a constant, but it can be uniquely determined as follows.

Since Vx Vb = 0, this velocity must be expressible as a gradient of some scalar potential function Фь (r).

Vb = Уфъ (2.9)

Setting the divergence of this Vb to zero as required by its definition gives

V – Vb = V – ^фъ) = 0

V2фb = 0 (2.10)

so that Фь must satisfy the Laplace equation (2.10). This will have a solution everywhere inside the flow-field if appropriate boundary conditions are specified on all the flow-field boundaries. The boundary conditions are case-dependent, and some typical examples are given below.

Фь = Vo ■ r = uo x + vo y + wo z (at distant boundary) (2.11)

дфb/dn = — (Vr + V) ■ n (at solid-wall boundary) (2.12)

For simple flat internal-flow boundaries such as wind tunnel walls, Vb can be alternatively obtained using the method of images. Many examples are given in Chapter 10.

It’s useful to note that the Vr superposition integral (2.4) has the form

Vr(r) = a(r’) K(r-r’) dx’ dy’ dz’	(2.13)
1 r — r’
K(r, r’) — K(r-r’) — /|3 4n | r—r’|3	(2.14)

where K is the kernel function which is strictly geometric, in that it depends only on the coordinates of the field point r and the integration point r’. More specifically, it depends only on the connecting vector r — r’ between the two points. The specific kernel function (2.14) can be interpreted as the velocity field V(r) of a unit-strength point source located at r’.