Adsorption-Controlled Model

Besides the collision-controlled quenching, an adsorbed oxygen molecule on a porous surface can also quench the luminescence; if this is the dominant mechanism, the oxygen quenching is controlled by adsorption and surface diffusion of the adsorbed oxygen on the porous surface. The oxygen concentration on a porous surface, [OJad, can be described by the fractional coverage of oxygen on the porous surface

Q [ O 2 ] ads

[O2] adsM

where [O2]adSM is the maximum oxygen concentration on the porous surface. The Stern-Volmer equation is then written as

I – _ 1 + kqT0[O2]adM Q, (2.38)

and accordingly the convenient form of the Stern-Volmer relation for aerodynamic applications is

Q

EaL _ A(T) + B(T)——, (2.39)

I Qref

The rate constant kq for the oxygen quenching, which is surface-diffusion – controlled, can be described by (Freeman and Doll 1983)

kq = 2nRAB *bd = К exP(-Esdiff /RT), (2.41)

where Rab is the relative distance between an adsorbed oxygen and an adsorbed luminophore, and D is the diffusivity and the parameter AB is a ratio of the modified first-order and second-order Bessel functions of the second kind. Basically, kq is temperature-dependent due to the Arrhenius relation

D = D0 eXP(-Esdiff /RT) .

To describe в, either the Langmuir isotherm or the Freundlich isotherm can be used (Carraway et al. 1991b). The Langmuir isotherm relates в to the partial pressure of oxygen pOq in the working gas by

b pO

в= °2 . (2.42)

1 + bPo2

The factor b in Eq. (2.42) is a function of temperature (Butt 1980)

The coefficient A[nngmut has the same temperature dependency as that for a conventional polymer PSP and that in the collision-controlled model, i. e.,

and the linearized form for Ar. is

Langmuir

Hence, Eq. (2.48) indicates that A[angmur is related to the temperature dependency of the non-radiative processes of the luminophore. On the other hand, B[amgmidr has the following temperature dependency

where E, — Esdiff + Eads. Rewriting Eq. (2.49) in an exponential form yields

and furthermore, linearization of Eq. (2.50) at T = T gives

Where El — E, – R Tref / 2 — Ediiff + E ads – RTref/ 2 . С^аГ^ the temperature

dependency of the coefficient B[angmiit, Eq. (2.51), is associated with both surface diffusion and adsorption; but it has the similar form to Eq. (2.23) for a conventional polymer layer. The reference Stern-Volmer coefficients ALangmuir, ref

and BLcngmuir, ref (their lengthy expressions are not given here) satisfy the

constraint Ahangmuir, ref + B Langmuir, ref = 1 .

The Freundlich isotherm can serve as another model for surface adsorption

0 — bp(Po2)r (2.52)

where the coefficient and exponent are

і RT

bf —~b= exp(-Eads /RT) and у ——————– . (2.53)

■^TY EadsM

The exponent /is an empirical parameter that is temperature-dependent. For a known yref at a known reference temperature Trep EdisU is given by

(2.54)
Substituting Eqs. (2.52), (2.53) and (2.54) into Eq. (2.39), we obtain the non-linear Stern-Volmer equation
(2.55)
where
(2.56)
and the linearized form for „иш1йЛ is
T – Tre T ref
(2.58)
AFreundlich = AFreundlich, ref
The coefficient BFremdlich has the temperature dependency kqbF(pO2ref)Y
(2.59)
Substituting Eqs. (2.41) and (2.53) into (2.59) yields
(2.60)
where Ef _ Esiiff + Eads. When an approximation Yref ~ Y is used for a small temperature change, the expression for BFreun<mch becomes
(2.61)
B Freundlich BFreundlich, ref ■

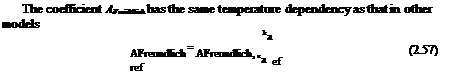which is similar to B^ . After rewriting all the terms in Eq. (2.61) in an

exponential form, linearization at T = Tref yields

where

Similar to the Langmuir-type model, the coefficient BFrmndlich has the temperature dependency associated with surface diffusion and adsorption. However, the photophysical model Eq. (2.55) describes the non-linear behavior of the Stern – Volmer plot for a porous PSP.