Approach
The equations for mathematical representation of a moving fluid are derived here for the most general case of an unsteady, compressible, viscous flow. It is most often the case that full generality is not required in a particular application. It may not be
|
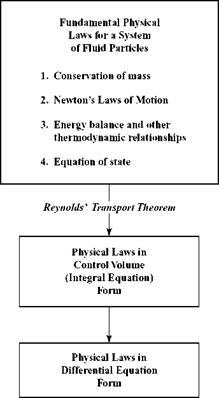
Figure 3.1. Procedure for development of equations of motion. |
necessary to account for compressibility effects in the flow over an airplane if the speed of flight is sufficiently low. Similarly, viscous forces may be negligible in some applications. An important skill emphasized in this chapter is the decision-making process used to reduce the general formulation to a simpler one that accounts for only the needed physical effects. In the examples mentioned, the density can be held constant if the flow is incompressible or the viscous terms can be dropped when frictional effects are not crucial. Such considerations may result in vast simplification of the mathematical problem.
The approach to be followed is illustrated in Fig. 3.1. We start by briefly reviewing the basic physical laws pertaining to conservation of mass, momentum, and energy. These are naturally expressed in familiar form by representing the behavior of a well-defined system of fluid particles. In this Lagrangian form, the equations are of limited use in handling the problems we address. What usually is needed is the effect of the motion of these particles on the forces of interaction on a body immersed in the flow. It is not required to determine a detailed history of the motion of the original group of fluid particles (i. e., the system) as it moves downstream. The Eul – erian control-volume approach as introduced in Chapter 2 provides a powerful tool for determining the properties of the fluid flow at any time and any location in the domain of interest. Review the definitions in Chapter 2 to understand the distinction between a Lagrangian and a Eulerian approach.
As indicated in Fig. 3.1, the first step is to translate the physical laws into control-volume form. The Reynolds’ Transport Theorem provides the mechanism for passing from the Lagrangian-system model to the more convenient Eulerian control-volume representation. The result is a set of integral equations that provide a useful way to describe the effects of fluid motion without knowledge of the details at each point in the region of interest. In other words, it gives an average or overall picture of the motion. There is a significant benefit here because the control volume can be defined in a variety of useful ways to fit the geometry of any particular problem. The shape and location of the boundaries of the control volume can be chosen to accommodate the required size and shape of the problem domain. A control volume can translate, accelerate, or rotate as necessary to fit the definition of the application. Any number of control volumes can be applied in a given problem to provide information about specific parts of the flow field.
Although in most applications we apply directly the differential equations of fluid motion in solving aerodynamics problems in later chapters, there are many useful and practical benefits of the intermediate control-volume integral formulation. The control-volume point of view often is a valuable tool in gaining physical understanding in a given situation before undertaking to solve the applicable differential equations. For example, if we need to determine only the total force acting on an object immersed in a flow, then this information frequently can be found without establishing all the details of the local-gas motion. If, however, we need to know how the fluid-interaction force elements that lead to this net force are distributed over the body, then a “sharper” representation is needed in which the local behavior of the fluid is determined. In this example, it may be necessary to find the actual distribution of pressure and viscous-shear forces over the body surface. This can be done only if we pass from the control-volume integral equation form to differential equation form so that we can study how the fluid properties change locally from point to point. Again, Fig. 3.1 illustrates the “plan of attack.” We use the integral control-volume equations to determine the underlying differential equations. As these analytical steps are carried out in this chapter, it is important to follow the procedure focusing mainly on the reduction from the general form to specific applications. The final result is a set of mathematical tools that enables the eventual solution of any fluid-dynamics problem. The remainder of the book is devoted to the application of these tools to analyze a wide variety of aerodynamics problems.