Boundary Conditions
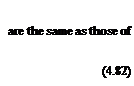 The boundary conditions associated with the TSD equation the linear models:
The boundary conditions associated with the TSD equation the linear models:
= U (f ‘±(x) – a)
Vф(x, z) ^ 0, x2 + z2
Note that the tangency condition is applied on the x-axis, which is consistent with the small disturbance assumption. For a lifting airfoil, the Kutta-Joukowski condition reads
Г'(с) = U < u(c, 0) >= U(u(c, 0+) – u(c, 0-)) = 0 (4.83)
where r(x) = U < ф(x, 0) >= U(ф(x, 0+) – ф(x, 0 )) represents the circulation distribution inside the profile.
4.1.2 Jump Conditions
The TSD is written as a system of two first-order PDEs in conservation form.
The jump conditions are given by
![]()
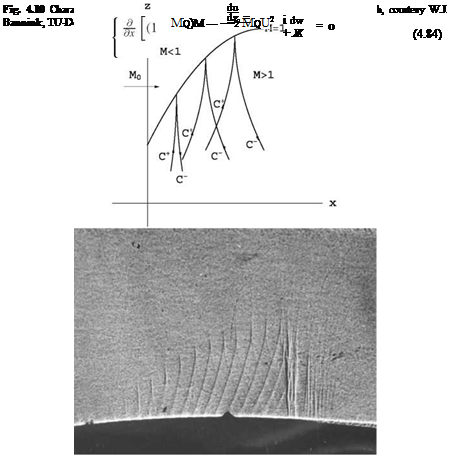 |
< (1 — M^)u — m02u2 > nx + < w > nz = 0
< w > nx — < u > nz = О
Upon elimination of n = (nx, nz), the unit vector normal to the jump line, the shock polar is obtained
The term in the first bracket can be written differently by using the identity < u2 >= 2u < u > where U = (u1 + u2)/2 represents the average value of u across the shock. This results in
^1 — M^ – (y + 1)M2u) < u >2 + < w >2= 0 (4.87)
Given the upstream state (u1,w1), if u < u*, the term in the bracket is positive and the only solution is the trivial solution < u >=< w >= 0. No jump is allowed and (u2, w2) = (u1; w1). The flow is locally subsonic. If u = u*, < w >= 0. This corresponds to a smooth transition through the sonic line if < u >= 0, or to the normal shock which does not deviate the flow since w2 = w1, if < u > = 0.
If u > u*, two solutions exist < w >= ±J(y + 1)M^yu1 – u* + < u >
corresponding to the two branches J + and J – of the polar. The maximum flow deviation through a shock occurs when < u >= 4(u* – u1)/3 and is given by
The shock polar is depicted in Fig.4.11.
The slopes of the shock waves in the physical plane are given by
![]() (dz ___________ 1___________
(dz ___________ 1___________
dx’J + ,J(y + 1)М2ум1 – u* +
![]() dz 1___________
dz 1___________
dx’J – J(y + 1)M0yu 1 – u* + <2>
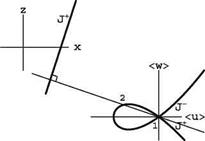
Note that the slopes of the lines that connect the downstream states to the double point O on the shock polar are perpendicular to the images of the shocks in the physical plane. In the limit of infinitely weak shocks, the tangents to the double point O are perpendicular to the characteristic lines representing them, Fig. 4.12.
![]()
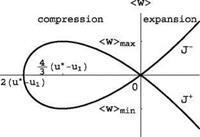 Fig.4.11 TSD polar
Fig.4.11 TSD polar
 |
Fig. 4.12 Polar in hodograph plane and shock in physical plane











