Constitutive Law and Strain Energy for Coupled Bending and Torsion

A straightforward way to introduce such coupling in the elementary beam equations presented previously is to alter the “constitutive law” (i. e., the relationship between cross-sectional stress resultants and the generalized strains). So, we change

where EI is the effective bending stiffness, GJ is the effective torsional stiffness, and K is the effective bending-torsion coupling stiffness (with the same dimensions as EI and GJ). Whereas EI and GJ are strictly positive, K may be positive, negative, or zero. A positive value of K implies that when the beam is loaded with an upward vertical force at the tip, the resulting positive bending moment induces a positive (i. e., nose-up) twisting moment. Values of GJ, EI, and K are best found by cross-sectional codes such as VABS™ a commercially available computer program developed at Georgia Tech (Hodges, 2006).

Now, given Eq. (2.58), it is straightforward to write the strain energy as

1.4.1 Inertia Forces and Kinetic Energy for Coupled Bending and Torsion

In general, there is also inertial coupling between bending and torsional deflections. This type of coupling stems from d, the offset of the cross-sectional mass centroid from the x axis shown in Fig. 2.7 and given by

so that the acceleration of the mass centroid is

For inhomogeneous beams, the offset d may be defined as the distance from the x axis to the cross-sectional mass centroid, positive when the mass centroid is toward the leading edge from the x axis.

Similarly, if one neglects rotary inertia of the cross-sectional plane about the z axis, the angular momentum of the cross section about c is

where, for beams in which the material density varies over the cross section, we may calculate the cross-sectional mass polar moment of inertia as

PIP = U p (y2 + z2) dA (2.63)

A

The kinetic energy follows from similar considerations and can be written di­rectly as

1.4.2 Equations of Motion for Coupled Bending and Torsion

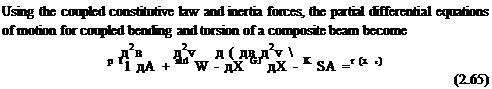д 2v д2в д2 д 2v дв

m дР + dдР + АР EIАР – K А* = f (x”)

where we see the structural coupling through K and the inertial coupling through d.

Of course, we may simplify these equations for isotropic beams undergoing coupled bending and torsion simply by setting K = 0.

Figure 2.8. Character of static-equili­brium positions