Critical Damping

Critical damping occurs when the system’s response decays to a very small number: At a certain frequency the system is able to dissipate all the energy from the external forcing. MacDonald, 1975, defines the critical damping as 1% of the steady state load response.

It is generally suggested that the decreasing admittance with the increasing frequency is due to the fact that the smaller turbulent eddies have a higher frequency, e. g. shorter wavelengths. However, we prove that this is also the

case for a laminar inviscidflow. A number of other events seem to occur. Past a critical damping frequency the transfer function increases again, and may reach several other minima. We have found no experimental data to substantiate this conclusion.

The existence of critical damping in this model is associated to a combi­nation of increasingly oscillatory Bessel functions. The first critical damping frequencies are kc ~ 5.13 for the circular plate and kc ~ 2.13 for the square plate, both with a gust speed ratio A = 1.

This result shows that the square plate is more effective in reducing the re­sponse from an unsteady forcing. For non-analytical bodies, critical frequen­cies may not exist.

With the assumption of small perturbations, critical damping will be associ­ated to a pressure wave of wavelength equal to the gust wavelength. When the latter one is a multiple of the plate’s chord, also the pressure distribution will have the same wavelength (with a time lag). When the gust wavelength Ag is equal to the chord c = 2b the following relationships hold:

cub ос 2тт/с it f Xg ttfVg Vg 1-А

V = zv = 2V = v = У7 = nV = 71 A

having assumed that the gust wavelength is related to its frequency by Ag = Vg /f. If there are n wavelength over the chord of the plate, the critical fre­quency is estimated from

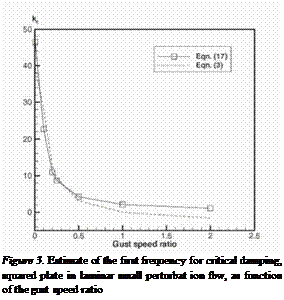If we plot the calculated data from Eq. 3 and the estimate, Eq. 16, we find a similar trend, although the values are not quite right, Fig. 3.

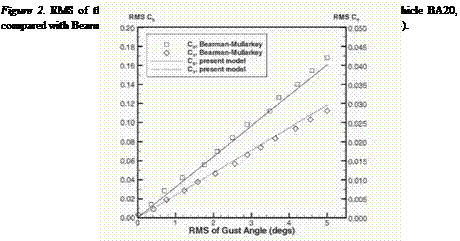
Bearman’s experiments (Bearman, 1971a), and Vickery’s theoretical corre­lations (Vickery, 1965) both refer to plates in normal turbulent fbw. These authors seem to imply that critical damping does exist in normal few condi­tions, at frequencies that are not discordant with the present ones (k < 10).

One key point evidenced by the experiments of Bearman et al. in turbu­lent ft>w is the fact that the admittance does not tend to one at the very long wavelengths.