. Influence of the Propulsive System on Trim and Pitch Stiffness

The influences of the propulsive system upon trim and stability may be both impor­tant and complex. The range of conditions to be considered in this connection is ex­tremely wide. There are several types of propulsive units in common use—recipro­
cating-engine-driven propellers, turbojets, turboprops, and rockets, and the variations in engine-plus-vehicle geometry are very great. The analyst may have to deal with such widely divergent cases as a high-aspect-ratio straight-winged airplane with six wing-mounted counterrotating propellers or a low-aspect-ratio delta with buried jet engines. Owing to its complexity, a comprehensive treatment of propulsive system influences on stability is not feasible. There does not exist sufficient theoretical or empirical information to enable reliable predictions to be made under all the above – mentioned conditions. However, certain of the major effects of propellers and propul­sive jets are sufficiently well understood to make it worth while to discuss them, and this is done in the following.

In a purely formal sense, of course, it is only necessary to add the appropriate di­rect effects, Cmo and dCmp/da in (2.3,21 and 22), together with the indirect effects on the various wing-body and tail coefficients in order to calculate all the results with power on.

When calculating the trim curves (i. e., elevator angle, tab angle, and control force to trim) the thrust must be that required to maintain equilibrium at the condition of speed and angle of climb being investigated (see Sec. 2.4). For example (see Fig. 2.1), assuming that aT < 1

Solving for CT, we get

CD + CL tan у 1 — aT tan у

Except for very steep climb angles, artan у <§ 1, and we may write approximately,

CT= CD + CL tan у (3.4,3)

Let the thrust line be offset by a distance zP from the CG (as in Fig. 3.5) and neglect­ing for the moment all other thrust contributions to the pitching moment except Tzp, we have

Now let CD be given by the parabolic polar (2.1,2), so that

cm„ = (C0min + KCL2 + C, tan y) — (3.4,5)

c

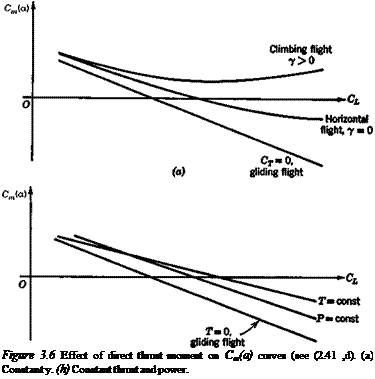
Strictly speaking, the values of CD and CL in (3.4,4 and 5) are those for trimmed flight, i. e. with Se = <5Cinm. For the purposes of this discussion of propulsion effects we shall neglect the effects of 8e on CD and CL, and assume that the values in (3.4,5) are those corresponding to 8e = 0. The addition of this propulsive effect to the Cm curve for rectilinear gliding flight in the absence of aeroelastic and compressibility effects might then appear as in Fig. 3.6a. We note that the gradient ~dCJdCL for any value of у > 0 is less than for unpowered flight. If dCJdCL is used uncritically as a criterion for stability an entirely erroneous conclusion may be drawn from such curves.

1. Within the assumptions made above, the thrust moment Tzp is independent of a, hence ЭCmJda = 0 and there is no change in the NP from that for unpow­ered flight.

2. A true analysis of stability when both speed and a are changing requires that the propulsive system controls (e. g., the throttle) be kept fixed, whereas each point on the curves of Fig. 3.6a corresponds to a different throttle setting. This parallels exactly the argument of Sec. 2.4 concerning the elevator trim slope.

(b)

For in fact, under the stated conditions, the Cm — CL curve is transformed into a curve of Setnm vs. V by using the relations дЄиіт = – Ст(а)ІС„щ and CL = W!pV2S. The slopes of Cm vs. CL and 8emm vs. V will vanish together.

If a graph of Cm vs. C, be prepared for fixed throttle, then у will be a variable along it, and its gradient dCJdCL is an index of stability, as shown in Sec. 6.4. The two idealized cases of constant thrust and constant power are of interest. If the thrust at fixed throttle does not change with speed, then we easily find

T zr Cm = — CL — m” W c

(3.4,6)

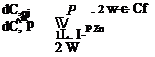If the power P is invariant, instead of the thrust, then T = P/V and we find

Thus in the constant thrust case, the power-off Cm — Cf graph simply has its slope changed by the addition of thrust, and in the constant power case the shape is changed as well. The form of these changes is illustrated in Fig. 3.6b and it is evident by comparison with 3.6a that the behavior of dCJdCL is quite different in these two situations.