Limit of Validity of Linearized Theories

The above linear theories all fail when the incoming Mach number approaches unity. Indeed, the Prandtl-Glauert correction shows a dependency of the local and global coefficients with incoming Mach number through the multiplication factor

1 /^J1 – m2, whereas, the linearized supersonic flow theory shows the correspond­ing dependency through the factor 1ЦM2 – 1. In both cases, the solution becomes infinite at M0 = 1. This is in contradiction with experiments that indicate, for exam­ple, that the lift and drag coefficients are finite and reach a maximum near M0 = 1. In graphic form, this is shown in Fig.4.9.

Fig. 4.8 Fuel pitch trim. a trimming fuel during transonic acceleration b trimming fuel during supersonic cruise c trimming fuel during transonic deceleration (from https://en. wikipedia. org/wiki/File: Concorde_fuel_trim. svg Author: steal88)

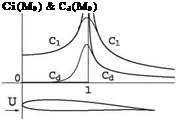Fig. 4.9 Linear theories and nonlinear transonic results near M0 = 1

The linearized potential equation does not allow for continuous description of flow fields from subsonic to supersonic flow regimes. In particular, it cannot represent flow fields in which regions of supersonic flow coexist with regions of subsonic flow, called mixed-type flows. Such complex flow fields, which may include sonic line, expansion wave and shock wave, require a mixed-type equation, one that is elliptic in regions of subsonic flow and hyperbolic where the flow is supersonic. In order to change type, such an equation has to be nonlinear. It will be presented in the next section. Note that near Mach one, the aerodynamic coefficients, as given by the nonlinear theory, reach an extremum. This is called “sonic freezing.”