Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Linear Inflow Models
A remarkable in-flight experiment to measure the time-averaged-induced velocity over the rotor disk in forward flight was made by Brotherhood & Stewart (1949). Based on measurements of the angular displacements of smoke streamers introduced upstream of the rotor, the longitudinal inflow variation was determined to be approximately linear. Some interesting aspects of the vortical wake can also be seen in the experiments [see also photo in Bramwell (1976), p. 131]. Similar results documenting the approximately linear longitudinal variation in the inflow were deduced by Heyson & Katsoff (1957). Since then, many experiments have confirmed the complicated nature of the inflow. During the transition from hover into level forward flight, that is, within the range 0.0 < д < 0.1, the induced velocity in the plane of the rotor is the most nonuniform, it being strongly affected by the presence of discrete tip vortices that sweep downstream near the rotor plane. In higher speed forward flight (pt > 0.15), the time-averaged longitudinal inflow becomes more linear and can be approximately represented by the variation
(3.175)
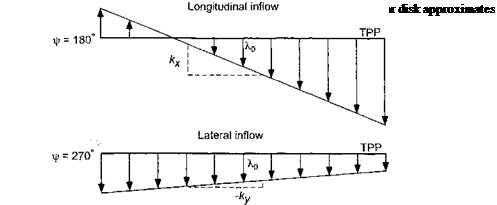
which is a form first suggested by Glauert (1926) – see Fig. 3.27. The coefficient Xq is the mean (average) induced velocity at the center of the rotor as given by the standard
(uniform) momentum theory where
X,- =k0 = — CL.——- . (3.176)
2^/Wx?
Glauert suggested that kx = 1.2, so that there is a small upwash at the leading edge of the rotor and an increase in downwash relative to the average value all along the trailing edge. This, of course, is similar to the chordwise downwash variation generated by a fixed-wing. A variation of Giauert’s result is to consider both a longitudinal and lateral variation in the inflow. In this case
 |
1 +kx— + ky^~ ) = Ao (1 кxr cos J/ – f kyr sin fr) . (3.177)
Here kx and ky can be viewed as weighting factors and represent the deviation of the inflow from the uniform value predicted by the simple momentum theory. From experiments with trimmed rotors, it is generally found that the inflow is heavily biased toward the rear of the disk and weakly biased toward the retreating side.
Various attempts have been made to directly calculate kx (and ky). One estimate can be found using an adaptation of linear momentum theory, as described by Payne (1959) and Johnson (1980) (see also Question 3.14). Weighting factors can also be estimated using rigid cylindrical vortex wake theories – see Coleman et al. (1945) and Johnson (1980) for a summary. One approximation for kx used by Coleman et al. (1945) is
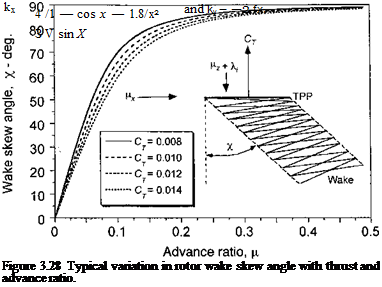
kx = tan ( ^ I, where the утке skew angle is x = tan-1 ( ——— |, (3.178)
2 / Дг+Хі/
and where )xx and iz are advance ratios defined parallel and perpendicular to the rotor disk (see Section 2.14.4 and Fig. 3.28). It is apparent that the skew angle increases rapidly with advance ratio, and for д > 0.2 the wake is relatively flat. Notice that for high-speed forward flight, kx approaches unity according to the above expression and does not represent the small region of upwash that is usually measured at the leading edge of the disk. Another parsimonious linear inflow model frequently employed in basic rotor analyses is attributed
 |
 |
to Drees (1949). In this model, the coefficients of the linear part of the inflow are obtained from another variation of vortex theory – see Johnson (1980) for a good summary. The inflow coefficients are given by
Drees’s model gives kx = 0 for ц, = 0, a maximum value of 1.11 at /л ^ 0.2, and Jcx slowly decreases thereafter. Like all of the other linear inflow models, Drees’s model is easy to implement in rotor analyses and gives a reasonably good description of the rotor inflow. Various other authors have suggested values for the coefficients in the Glauert model, which are summarized in Table 3.1. Payne (1959) suggests a value for kx based on the numerical results of Castles & De Leeuw (1954), which approaches 4/3 at high advance ratios, and in light of the experimental evidence appears to be one of the better representations of the longitudinal inflow distribution. Overall, the Drees (1949), Payne (1959), and Pitt & Peters (1981) models are found to give the best representation of the inflow gradient as functions of the wake skew angle and the advance ratio when compared to the experimental evidence.
|
Table 3.1. Various Estimated Values of First Harmonic Inflow
|
