Lines

The second lumping stage consists of dividing the s coordinate into some number of short intervals, and assuming that r/(s, i) — r'(so, i) where so is some representative s value on each interval. We can then integrate A or y across each interval from si to s2, thus defining the line or filament strengths Л(і) or Г(і). Each surface integral then becomes a summation over a number of simpler line integrals along the remaining

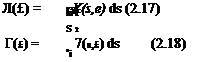filament coordinate £, with r'(£) now denoting the integration points on the filament. Here we also assume that £ is chosen to be aligned locally with the 7 vector direction, as indicated in Figure 2.3.

The resulting velocity fields Va and Vr defined above are now strongly singular at the filaments, varying as |Va|, |Vr| ~ 1/Ar where Ar is the nearest distance to a filament. The magnitude of these singularities depends on the width of the s intervals for the lumping integration and the resulting line spacing, which can be chosen arbitrarily. A fine sheet subdivision into many weak filaments proportionally reduces the singularities, giving a smoother velocity field at any given distance from the filament-approximated surface.

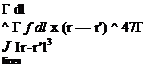The vortex-filament velocity definition (2.18) can be simplified somewhat by applying the Helmholtz vortex law [2] which states that the magnitude of Г cannot change along the filament. In addition, since the £ coordinate was chosen to be aligned with 7, the lumped Г must be parallel to the filament element vector dl at each location. We can then convert the Vr definition (2.18) into the familiar Biot-Savart integral.

Note that the integral itself is purely geometric, and can be evaluated without knowing the filament circula­tion Г a priori.