Modeling a Fluid at Rest

Because there is no motion, the ideas of statics yield the information that we need. That is, simple force and moment balances provide all of the necessary relation­ships among variables. In a fluid such as a gas, the forces acting on a fluid element are related to pressure or possibly to surface tension. Viscous forces do not appear because they depend on the presence of a velocity gradient.

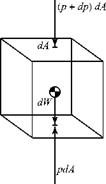
Consider the fluid element shown in Fig. 2.7.

This rectangular element has cross-sectional area dA normal to the vertical axis, z. Only the forces in the z-direction are shown because all forces in the lateral direc­tion are mutually balanced. As the figure suggests, the weight of the element, dW, is balanced by the pressure forces acting on the faces of the element. This provides a way to determine how the pressure changes in a body of fluid such as a water tank or the earth’s atmosphere. We use the latter application to illustrate the principles involved.

For static equilbrium in the vertical directions, it is necessary that I F = 0, so that:

pdA – (p + dp)dA – dW = 0. (2.27)

Because the mass of the element is equal to the volume times the density of the material inside, we can write the differential weight as dW = dmg = (pdV)g, where g is the local acceleration due to gravity. If the height of the element is dz, then the volume is dV = dAdz, and the force balance yields dp + pgdz = 0, which can be expressed in differential-equation form as:

This result is often called the hydrostatics equation and it shows how pressure and density are interrelated when there is no motion of the fluid. If the density is known as a function of pressure and the gravitational acceleration is known as a function of z, this equation can be integrated to yield information about the pressure as a func­tion of z. In our application, we interpret z = h to be measured from the earth’s sur­face; it is referred to as the geometric altitude. There are other definitions for altitude that may be useful on occasion. For example, we refer to the pressure altitude as the altitude corresponding to a standard atmospheric value for the static pressure meas­ured outside the vehicle. Equation 2.28 indicates that if the density and gravity were constant, the pressure would decrease linearly with altitude. However, this does not account for observable features of the atmosphere; effects of temperature and den­sity changes also must be considered.