Nondimensional Coefficients

Before developing the analysis further, it is timely to introduce the concept of nondimensional coefficients. Just as does the airplane aerodynamicist, the helicopter aerodynamicist finds it convenient to work with nondimensional coefficients to define rotor characteristics in a form that is independent of rotor size. For this purpose, the system used by NASA will be adopted:.

рЛ(Ш)3

One of the convenient features of this set of coefficients is that the torque and power coefficients are numerically equal. This may be shown by writing the equation for power, P, in ft lb/sec as:

Substituting this into the equation for CP gives:

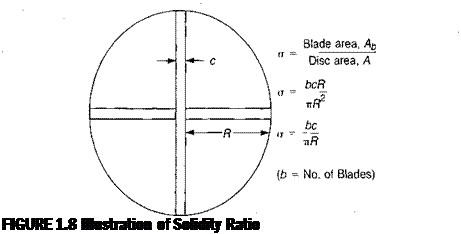
Note that the reference area for each of these rotor coefficients is the. rotor disc area, A. It is often desirable to use coefficients based on blade area rather than on disc area. In order to do this, the rotor solidity ratio, G, is defined:

Total blade area

G = ——- ■;————-

Disc area

As shown in Figure 1.8, the solidity is the amount of the rotor disc made solid by the blades:

Ab bcR be

A nP2 TR

For the example helicopter:

120 (4)(2)

———- = ww- = 0.085

2,827 n(30)

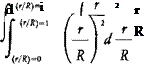
Note that in using this definition, the blades are assumed to extend into the center of rotation where some overlapping of blade area occurs. This assumption is used in the definition of solidity even though, in practice, the actual blade sections do not start until some distance from the center of rotation. This is a satisfactory assumption since the inboard portions of the blades contribute little to the aerodynamic characteristics of the rotor. However, the same cannot be said about the outboard portions of the rotor. If the blade is tapered, the aerodynamic biasing toward the tips should be accounted for by rewriting the equation for solidity to define a thrust-weighted solidity as:

K_

nR

where

and c is the local chord.

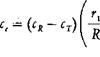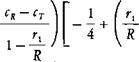For example, a blade planform might consist of a portion with a constant chord, cR, from the root to a point, rXi and then taper linearly to a tip chord of cT. The equation for the effective thrust weighted chord in this case is:

The rotor coefficients based on effective blade area are:

An analogy with airplane aerodynamics is that CT corresponds to span loading and governs induced power. On the other hand, CT/c corresponds to lift coefficient, and its value is used to determine the margin to blade stall just as CL is compared to

CLmix – The numerical value of CT/o may be related to an average two-dimensional lift coefficient,?/, by defining the lift per running foot as a function of the average lift coefficient, which for this purpose will be assumed to be constant along the blade:

AL

a7

Integrating out the blade and multiplying by the number of blades gives an expression for rotor thrust:

T = £-f22C/f| r2dr = — (ClR)2bcRcі

‘ 2 JQ 6

but by definition:

T = pbcR(ClR)2CT/o Equating these two equations gives:

С/ = 6CT/o

Most airfoils used for rotor blades at operational Reynolds and Mach numbers have maximum lift coefficients of between 1.0 and 1.4. Thus the maximum value of CT/o that may be developed before reaching blade stall is between 0.17 and 0.23. For the example helicopter at sea level with a vertical drag penalty of 4 percent, the value of Cr/a is:

(20,000)(1.04)

(.002377)(4)(2)(30)(650)2

and the corresponding average lift coefficient, ct is:

c,= 6(0.086) = 0.52

If the airfoil has a maximum lift coefficient of 1.2, the rotor can lift more than twice the design gross weight of the helicopter before stalling. At 25,000 ft, however, the average lift coefficient is 1.14, and the rotor is on the verge of stall.