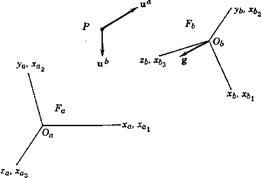
NOTATION

Let Fn and Fh be two right-handed reference frames, with coordinate axes denoted as in Fig. 4.1. Note that two alternative systems are used: (x, y, z) or (xv x2, ,r3), the choice at any time being governed by custom and

convenience. In general the two frames have relative motion, both linear and angular.

Consider now the description of a typical vector which does not depend on the motion of the frame of reference. For example let Fa be the Earth, Fb a moving rigid vehicle, and the vector in question be the gravitational force exerted by the former on the latter, represented by g in Fig. 4.1. The vector g is the same for observers in both Fa and Fb in the sense that they would both find it to be of the same magnitude, and of the same orientation relative to any third frame. The components of g along the axes of Fa and Fb are of course in general dilferent, and we denote them by

(How to calculate one set of components from the other is treated in Sec. 4.4.)

A more complicated situation arises when we consider vectors that do depend on the motion of the reference frame, i. e. that are not the same for two observers, one in Fa and the other in Fb. For example, consider the veloc­ities of a point P relative to Fa and Fb. These are two different vectors, each of which may have its components given in the directions of either set of axes, leading to four sets of components.

The practice followed in this text is to use different symbols for physically different vectors, or appropriate subscripts or superscripts. Thus to usually represents the angular velocity of a reference frame relative to inertial space, and a superscript identifies the rotating frame. For example toB is the angular velocity of an Earth-fixed frame FE. Again, v0 and vc give the inertial veloci­ties of points 0 and G, the frame of reference for components being identified with a further subscript, so that v0 is the column matrix of the components of v0 along the axes of Fw (wind axes).

In the example of Fig. 4.1, we may let u® be the velocity of P relative to Fa and ub its velocity relative to Fb. The four sets of components are then

V, V and иЛ иь

each being a column matrix as in (4.1,1).

It should he emphasized that the transformation that transforms u® into ub is quite different from that which transforms ua® into ub®, and the two should not he confused (see Sec. 4.6).

Notwithstanding the above general rules, certain exceptions to this form of notation are made in the subsequent treatments. These are in conformity with a long tradition of usage in flight dynamics, and bring the main equations derived into harmony with most past and current North American literature on the subject.